题目内容
已知
，a
、b
Î
(0，p
)，求2a
－b
的值．
答案：略
解析：
提示：
解析：
|
解：∵  ， ，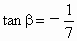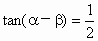
∴ 
∵  ，∴ ， ，
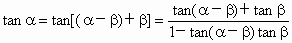
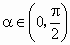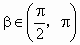∴a －b Î (－p ，0)∵  ，∴ ，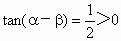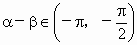
2a －b =a ＋(a －b )Î (－p ，0)． 而tan(2a
－b
)=1，∴ 已知a －b 及b 角的正切，显然要求2a －b 的正切，该题必须通过角变换，2a －b =a ＋(a －b )，a =(a －b )＋b ，故需先求出a 角的正切． |
，
．提示：
|
该小题的解题思路是利用角变换求出了 2a －b 角的正切值，难点和关键是通过判断值的大小缩小2a －b 角的范围．若仅仅根据已知条件告诉的a 和b 的范围判断2a －b 的范围，这个范围是非常大的，这个范围是(－p ，p )则正切值为1的角有 和 ，导致错误答案． |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，a
Î
(0，2p
)，
，求tanb
及tan(2a
－b
)．
的两个实数根，求
．