题目内容
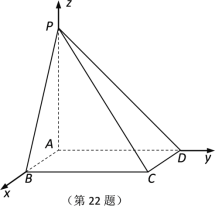
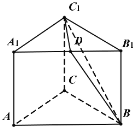
【题目】我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称之为堑堵;将底面为矩形且一侧棱垂直于底面的四棱锥称之为阳马;将四个面均为直角三角形的四面体称之为鳖臑[biē nào].某学校科学小组为了节约材料,拟依托校园内垂直的两面墙和地面搭建一个堑堵形的封闭的实验室![]() ,
,![]() 是边长为2的正方形.
是边长为2的正方形.


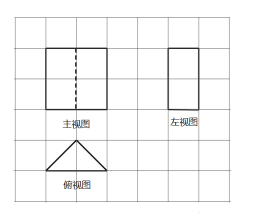
(1)若![]() 是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
(2)若![]() ,
,![]() 在
在![]() 上,证明:
上,证明:![]() ,并回答四面体
,并回答四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)当阳马![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)答案见解析(2)答案见解析(3)![]()
【解析】
(1)根据其几何体特征,即可画出其三视图.
(2)证明![]() ,结合
,结合![]() ,即可得到
,即可得到![]() 面
面![]() ,进而可证明
,进而可证明![]() .
.
(3)阳马![]() 的体积为:
的体积为:![]() ,根据均值不等式可得:
,根据均值不等式可得:![]() (
(![]() 取得等号),即可求得
取得等号),即可求得![]() .以点
.以点![]() 为顶点,以
为顶点,以![]() 底面求三棱锥
底面求三棱锥![]() 体积, 在以点
体积, 在以点![]() 为顶点,以
为顶点,以![]() 底面求三棱锥
底面求三棱锥![]() 体积.利用等体积法即可求得点
体积.利用等体积法即可求得点![]() 到平面
到平面![]() 的距离.
的距离.
(1)画出堑堵的三视图:
(2)
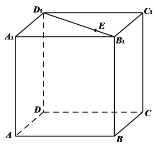
如图,连接![]() 和
和![]() .
.
![]() 由题意可知:
由题意可知:![]() 面
面![]() ,
,![]() 在平面
在平面![]()
![]()
![]()
又![]()
![]()
![]() 面
面![]() 故:
故: ![]() ,可得
,可得![]() 为直角三角形.
为直角三角形.
![]() 由题意可知
由题意可知![]() ,
,![]() ,
,![]() 都是直角三角形.
都是直角三角形.
![]() 四面体
四面体![]() 四个面都是直角三角形,故四面体
四个面都是直角三角形,故四面体![]() 是鳖臑.
是鳖臑.
(3)
![]() 在
在![]() 中,
中,![]()
根据均值不等式可得:![]() (
(![]() 取得等号)
取得等号)
![]() 由题意可知,
由题意可知,![]() 面
面![]()
![]() 阳马
阳马![]() 的体积为:
的体积为:![]()
(![]() 取得等号)
取得等号)
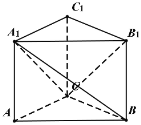
以![]() 为顶点,以
为顶点,以![]() 底面求三棱锥
底面求三棱锥![]() 体积:
体积:
![]()
![]()
![]()
![]() ,设
,设![]() 到面
到面![]() 距离为
距离为![]()
以![]() 为顶点,以
为顶点,以![]() 底面求三棱锥
底面求三棱锥![]() 体积:
体积:
![]()
![]()
![]() 解得:
解得:![]()

练习册系列答案
相关题目