题目内容
如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA⊥面ABCD,PA=AC=a,PB=PD=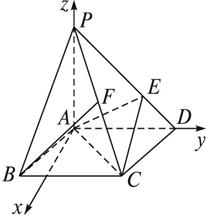
解法一:当F是棱PC的中点时,BF∥平面AEC.
因为![]()
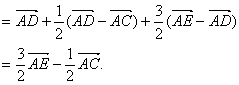
所以![]() 、
、![]() 、
、![]() 共面.
共面.
又BF![]() 平面AEC,从而BF∥平面AEC.
平面AEC,从而BF∥平面AEC.
解法二:如图,以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直于平面PAD的直线为x轴,建立空间直角坐标系.

由题意,知相关各点的坐标分别为
A(0,0,0),B(![]() a,-
a,-![]() a,0),C(
a,0),C(![]() a,
a,![]() a,0),D(0,a,0),P(0,0,a),E(0,
a,0),D(0,a,0),P(0,0,a),E(0,![]() a).
a).
所以![]() =(0,
=(0,![]() ),
),
![]() ,
,
![]()
设点F是棱PC上的点,![]() 其中0<λ<1,
其中0<λ<1,
则![]()
令![]()
得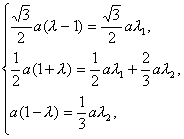
即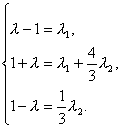
解得λ=![]() ,λ1=-
,λ1=-![]() ,λ2=
,λ2=![]() ,
,
即λ=![]() 时,
时,![]() ,即F是PC的中点时,
,即F是PC的中点时,![]() 、
、![]() 、
、![]() 共面.
共面.
又BF![]() 平面AEC,所以当F是棱PC的中点时,
平面AEC,所以当F是棱PC的中点时,
BF∥平面AEC.
解法三:由解法二可知![]()
![]()
设平面ACE的法向量为n=(x,y,z),
则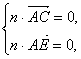
即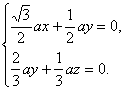
令y=1,得z=-2,x=-![]() ,即n=(-
,即n=(-![]() ,1,-2).
,1,-2).
设![]()
∴F点的坐标为(![]() aλ,
aλ,![]() aλ,a-aλ).
aλ,a-aλ).
∴![]()
∴![]()
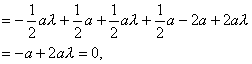
∴λ=![]() ,即
,即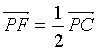 .
.
又∵BF![]() 平面AEC,
平面AEC,
∴当F是棱PC的中点时,BF∥平面AEC.
解法四:当F是棱PC的中点时,BF∥平面AEC.
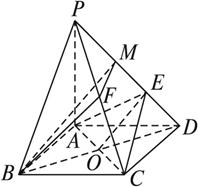
如图,取PE的中点M,连结FM,则FM∥CE. ①
由EM=![]() PE=ED,知E是MD的中点,
PE=ED,知E是MD的中点,
∴BM∥OE. ②
由①②,知平面BFM∥平面AEC,
又BF![]() 平面BFM,∴BF∥平面AEC.
平面BFM,∴BF∥平面AEC.

练习册系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.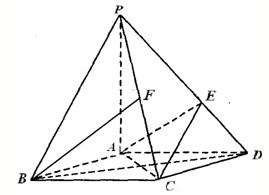 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2