题目内容
已知E(2,2)是抛物线C:y2=2px上一点,经过点(2,0)的直线l与抛物线C交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N,则∠MON的大小为________.

将E(2,2)的坐标代入y2=2px,得p=1,所以抛物线方程为y2=2x.
设A ,B
,B ,M(xM,xN),直线l方程为x=my+2,
,M(xM,xN),直线l方程为x=my+2,
与抛物线方程联立得 消去x,得y2-2my-4=0,
消去x,得y2-2my-4=0,
则由韦达定理得y1y2=-4,y1+y2=2m.
直线AE的方程为y-2= (x-2),即y=
(x-2),即y= (x-2)+2,
(x-2)+2,
令x=-2,得yM= .同理可得yN=
.同理可得yN= .
.
又 =(-2,yM),
=(-2,yM), =(-2,yN),
=(-2,yN),
 ·
· =4+yMyN=4+4
=4+yMyN=4+4 =
=
4+ =0.
=0.
所以 ⊥
⊥ ,即∠MON为定值
,即∠MON为定值 .
.
设A
 ,B
,B ,M(xM,xN),直线l方程为x=my+2,
,M(xM,xN),直线l方程为x=my+2,与抛物线方程联立得
 消去x,得y2-2my-4=0,
消去x,得y2-2my-4=0,则由韦达定理得y1y2=-4,y1+y2=2m.
直线AE的方程为y-2=
 (x-2),即y=
(x-2),即y= (x-2)+2,
(x-2)+2,令x=-2,得yM=
 .同理可得yN=
.同理可得yN= .
.又
 =(-2,yM),
=(-2,yM), =(-2,yN),
=(-2,yN), ·
· =4+yMyN=4+4
=4+yMyN=4+4 =
=4+
 =0.
=0.所以
 ⊥
⊥ ,即∠MON为定值
,即∠MON为定值 .
.
练习册系列答案
相关题目
 ,0),直线l:x=-
,0),直线l:x=-
 上一点
上一点 的纵坐标为4,则点
的纵坐标为4,则点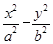 =1(a>0,b>0)的两条渐近线围成一个等腰直角三角形,则该双曲线的离心率是( )
=1(a>0,b>0)的两条渐近线围成一个等腰直角三角形,则该双曲线的离心率是( )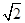
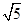
 的焦点
的焦点 作倾斜角为
作倾斜角为 的直线与抛物线分别交于
的直线与抛物线分别交于 ,
, 两点(
两点( 轴左侧),则
轴左侧),则 .
.