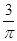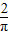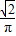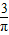题目内容
在半径为1的圆内随机地取一条弦,问其长超过圆内接等边三角形的边长的可能性(概率)是多少?
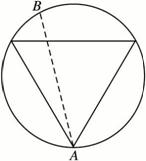
解法一:任何弦交圆周两点,不失一般性先固定其中一点于圆周上,以此点为顶点作一等边三角形,显然只有通过此三角形内的弦才满足要求,这种弦的另一端跑过的弧长为整个圆周的![]() ,故所求的概率为
,故所求的概率为![]() .
.
解法二:弦长跟它与圆心的距离有关,当且仅当它与圆心的距离小于![]() 时,其长才大于
时,其长才大于![]() ,因此所求的概率为
,因此所求的概率为![]() .
.

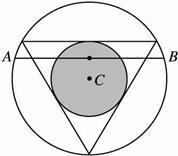
解法三:弦被其中点唯一确定,当且仅当其中点属于半径为![]() 的同心圆时,弦长大于
的同心圆时,弦长大于![]() ,此小圆的面积为大圆面积的
,此小圆的面积为大圆面积的![]() ,故概率等于
,故概率等于![]() .
.
说明:同一问题有三种不同的答案,原因在于取弦时采用不同的等可能性假定!在第一种解法中,假定端点在圆周上均匀分布,在第二种解法则假定弦的中点在直径上均匀分布,而在第三种解法又假定弦的中点在圆内均匀分布.这三种答案是针对三种不同的随机试验,对于各自的随机试验而言,它们都是正确的.因此在使用术语“随机”“等可能”“均匀”时,应明确指明其含义;这又因试验而异,须细细体会.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
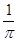 B、
B、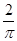 C、
C、 D 、
D 、