题目内容

(1)设x＞－1，试比较ln(1＋x)与x的大小；

(2)是否存在常数a∈N，使得对任意大于1的自然数n都成立？若存在，试求出a的值并证明你的结论；若不存在，请说明理由．

答案：
解析：

　　解：(Ⅰ)设，则，

　　当时，，单调递减；

　　当时，，单调递增；

　　故函数有最小值，则恒成立　4分

　　(Ⅱ)取进行验算：

　　

　　

　　

　　

　　猜测：①，

　　②存在，使得恒成立．　6分

　　证明一：对，且，

　　有

　　

　　

　　

　　

　　

　　又因，

　　故　8分

　　从而有成立，即

　　所以存在，使得恒成立　10分

　　证明二：

　　由(1)知：当时，，

　　设，，

　　则，所以，，，

　　当时，再由二项式定理得：

　　

　　即对任意大于的自然数恒成立，　8分

　　从而有成立，即

　　所以存在，使得恒成立　10分


练习册系列答案
相关题目
设函数f（x）=x2+1，g（x）=x，数列{an}满足条件：对于n∈N*，an＞0，且a1=1并有关系式：f（an+1）-f（an）=g（an+1），又设数列{bn}满足bn=
log
a
an+1
（a＞0且a≠1，n∈N*）．
（1）求证数列{an+1}为等比数列，并求数列{an}的通项公式；
（2）试问数列{
1
bn
}是否为等差数列，如果是，请写出公差，如果不是，说明理由；
（3）若a=2，记cn=
1
(an+1)-bn
，n∈N*，设数列{cn}的前n项和为Tn，数列{
1
bn
}的前n项和为Rn，若对任意的n∈N*，不等式λnTn+
2Rn
an+1
＜2(λn+
3
an+1
)恒成立，试求实数λ的取值范围．
（附加题）设函数f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的x，y∈R，都有f（x+y）=f（x）f（y）．
（1）求f（0），判断函数f（x）的单调性；
（ 2 ）数列{an}满足a1=f（0），且f(an+1)=
1
f(-2-an)
（n∈N*）
A．求数列{an}的通项公式；
B．令bn=(
1
2
)an，Sn=b1+b2+b3+…bn，Tn=
1
a1a2
+
1
a2a3
+…+
1
anan+1
，试比较Sn与
2
3
Tn的大小，并加以证明．
（2006•宝山区二模）先看下面的例题：将5050折分成若干个连续整数之和．因为5050是偶数，所以不能分成两个连续整数之和．若分成三个连续整数之和，设为x-1，x，x+1，则3x=5050，无解．若分成四个连续整数之和，设为x-1，x，x+1，x+2，则x-1+x+x+1+x+2=5050，解得x=1262，所以，5050=1261+1262+1263+1264．按照上述思路，还有其它分法．将1815折分成若干个连续整数之和，试给出1815的至少三种折分
907+908
907+908
、
604+605+606
604+605+606
、
361+362+363+364+365
361+362+363+364+365
．

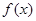设函数是定义在［－1，0）∪（0，1］上的奇函数，当x∈［－1，0）时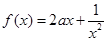，（a∈R).

（1）当x∈(0，1］时，求的解析式；

（2）若a＞－1，试判断在（0，1）上的单调性，并证明你的结论；

（3）是否存在a，使得当x∈（0，1）时，f(x)有最大值－6.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网