题目内容
已知实数a<b<c,设方程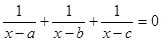 的两个实根分别为
的两个实根分别为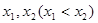 ,则下列关系中恒成立的是( ).
,则下列关系中恒成立的是( ).
A.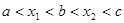 | B.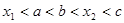 |
C.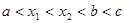 | D.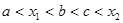 |
A
解析试题分析: 因为根据题意实数a<b<c,而且方程
那么根据已知中两个实根分别为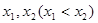 ,那么必然有判别式大于零,同时结合根与次数的关系可知
,那么必然有判别式大于零,同时结合根与次数的关系可知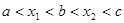 ,选A.
,选A.
考点:本题主要考查了函数与不等式的综合运用,是一道中档试题。
点评:解决该试题的关键是方程有解时,确定解与系数的关系的运用,要变形化简结合二次函数的 性质来分析得到。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
若 且
且 ,则下列不等式中一定成立的是( )
,则下列不等式中一定成立的是( )
A. | B. | C. | D. |
下面四个条件中,使 成立的必要而不充分的条件是( )
成立的必要而不充分的条件是( )
A. | B. | C. | D. |
已知实数 、
、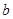 、
、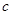 满足
满足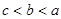 ,且
,且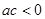 ,那么下列不等式一定成立的是
,那么下列不等式一定成立的是
A.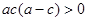 | B.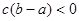 | C.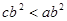 | D.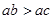 |
三个数 ,
, ,
, 的大小顺序为( )
的大小顺序为( )
A. | B. | C. | D. |
当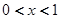 时,则下列大小关系正确的是( )
时,则下列大小关系正确的是( )
A. | B.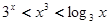 |
C.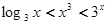 | D.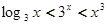 |
关于 的不等式
的不等式 的解集是( )
的解集是( )
| A.(-2,3) | B.(-3,2) |
C.( ) ) (3, (3, ) ) | D. |
 和
和 的解集分别为
的解集分别为 和
和 ,那么称这两个不等式为对偶不等式. 如果不等式
,那么称这两个不等式为对偶不等式. 如果不等式 与不等式
与不等式 为对偶不等式,且
为对偶不等式,且 ,则
,则 .
.