题目内容
()(本小题满分13分)
已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的导函数
的导函数![]() ;
;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 是
是![]() 上的增函数,求
上的增函数,求![]() 的最小值;
的最小值;
(Ⅲ)当![]() ,
,![]() 时,函数
时,函数![]() 在
在![]() 上存在单调递增区间,求
上存在单调递增区间,求![]() 的取值范围.
的取值范围.
(Ⅰ)![]() (Ⅱ)当
(Ⅱ)当![]() ,且
,且![]() 时,
时,![]() 取得最小值
取得最小值![]() (Ⅲ)
(Ⅲ)![]() 的取值范围是
的取值范围是![]() .
.
解析:
Ⅰ)解:![]() . …………………………………3分
. …………………………………3分
(Ⅱ)因为函数![]() 是
是![]() 上的增函数,所以
上的增函数,所以![]() 在
在![]() 上恒成立.
上恒成立.

则有![]() ,即
,即![]() .
.
设![]() (
(![]() 为参数,
为参数,![]() ),
),
则![]() .
.
当![]() ,且
,且![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
(可用圆面的几何意义解得![]() 的最小值
的最小值![]() ) ………………………8分
) ………………………8分
(Ⅲ)①当![]() 时,
时,![]() 是开口向上的抛物线,显然
是开口向上的抛物线,显然![]() 在
在![]() 上存在子区间使得
上存在子区间使得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
②当![]() 时,显然成立.
时,显然成立.
![]() ③当
③当![]() 时,
时,![]() 是开口向下的抛物线,要使
是开口向下的抛物线,要使![]() 在
在![]() 上存在子区间使
上存在子区间使![]() ,应满足
,应满足  或
或
解得![]() ,或
,或![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
则![]() 的取值范围是
的取值范围是![]() . …………………………………………13分
. …………………………………………13分

练习册系列答案
相关题目
(本小题满分13分)
随机变量X的分布列如下表如示,若数列 是以
是以 为首项,以
为首项,以 为公比的等比数列,则称随机变量X服从等比分布,记为Q(
为公比的等比数列,则称随机变量X服从等比分布,记为Q( ,
, ).现随机变量X∽Q(
).现随机变量X∽Q( ,2).
,2).
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求随机变量X的数学期望EX;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
 经过点
经过点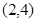 .
.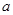 的值;(2)求
的值;(2)求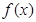 在[0,1]上的最大值与最小值.
在[0,1]上的最大值与最小值.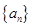 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,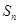 为
为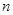 项和.
项和.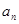 及
及 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列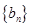 的通项公式及其前
的通项公式及其前 .
.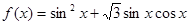

 的最小正周期和值域;
的最小正周期和值域; 的图象按向量
的图象按向量 平移后得到函数
平移后得到函数 的图
象,求函数
的图
象,求函数 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且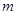 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出

