题目内容
若向量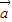 =(2,-3),
=(2,-3),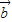 =(1,-2),向量
=(1,-2),向量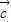 满足
满足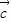 ⊥
⊥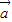 ,
,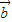 •
•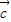 =1,则
=1,则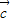 的坐标为 .
的坐标为 .
【答案】分析:设出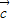 =(x,y),根据
=(x,y),根据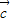 与所给的两个向量之间的垂直和数量积为1两个条件,利用坐标形式的数量积公式写出关于x和y的方程组,解方程组即可得到向量的坐标.
与所给的两个向量之间的垂直和数量积为1两个条件,利用坐标形式的数量积公式写出关于x和y的方程组,解方程组即可得到向量的坐标.
解答:解:设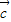 =(x,y)
=(x,y)
∵向量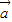 =(2,-3),
=(2,-3),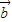 =(1,-2),
=(1,-2),
向量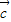 满足
满足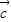 ⊥
⊥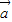 ,
,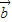 •
•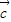 =1,
=1,
∴2x-3y=0,
x-2y=1
∴x=-3,y=-2,
∴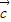 =(-3,-2)
=(-3,-2)
故答案为:(-3,-2)
点评:本题考查坐标形式的向量的数量积运算,考查两个向量垂直,是一个基础题,在解题时主要应用向量的坐标形式,这样题目变成简单的数字的运算.
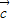 =(x,y),根据
=(x,y),根据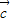 与所给的两个向量之间的垂直和数量积为1两个条件,利用坐标形式的数量积公式写出关于x和y的方程组,解方程组即可得到向量的坐标.
与所给的两个向量之间的垂直和数量积为1两个条件,利用坐标形式的数量积公式写出关于x和y的方程组,解方程组即可得到向量的坐标.解答:解:设
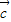 =(x,y)
=(x,y)∵向量
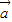 =(2,-3),
=(2,-3),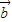 =(1,-2),
=(1,-2),向量
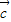 满足
满足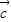 ⊥
⊥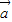 ,
,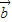 •
•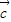 =1,
=1,∴2x-3y=0,
x-2y=1
∴x=-3,y=-2,
∴
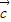 =(-3,-2)
=(-3,-2)故答案为:(-3,-2)
点评:本题考查坐标形式的向量的数量积运算,考查两个向量垂直,是一个基础题,在解题时主要应用向量的坐标形式,这样题目变成简单的数字的运算.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
若向量a=(2,-3,1),b=(2,0,3),c=(0,2,2),则a•(b+c)=( )
| A、4 | B、15 | C、7 | D、3 |
若向量
=(2,3),
=(x,-6),且
∥
,则实数x=( )
| a |
| b |
| a |
| b |
| A、-4 | B、4 | C、-6 | D、6 |