题目内容
12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排，若其他人的相对顺序不变，则不同调整方法的总数是 ( )
A． | B． | C． | D． |
C
解析试题分析：第一步从后排8人中选2人有
种方法，第二步6人前排排列，先排列选出的2人有
种方法，再排列其余4人只有1种方法，因此所有的方法总数的种数是
考点：排列组合
点评：此类题目的求解一般遵循先选择后排列，结合分步计数原理的方法
练习册系列答案
相关题目
(1-x)3(1-
)3展开式中常数项是( )
| A．－20 | B．18 | C．20 | D．0 |
把一同排6张座位编号为1，2，3，4，5，6的电影票全部分给4个人，每人至少分1张，至多分2张，且这两张票具有连续的编号，那么不同的分法种数是
| A．168 | B．96 | C．72 | D．144 |
二项式
的展开式的第二项的系数为
，则
的值为（ ）
A． | B． | C．或 | D．或 |
某大学的8名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽车.每车限坐4名同学(乘同一辆车的4名同学不考虑位置)，其中大一的孪生姐妹需乘同一辆车，则乘坐甲车的4名同学中恰有2名同学是来自于同一年级的乘坐方式共有
| A．24种 | B．18种 | C．48种 | D．36种 |
(1+2x) 6的展开式中，x的系数等于
，则函数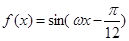
的最小正周期是
A． | B． | C． | D． |
二项式
的展开式中常数项是
| A．28 | B．-7 | C．7 | D．-28 |
的展开式中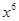
的系数是（ ）
A． | B． | C． | D． |