题目内容
【题目】在平面直角坐标系![]() 中,
中, ![]() 分别为椭圆
分别为椭圆![]() :
: ![]() 的左、右焦点,
的左、右焦点, ![]() 为短轴的一个端点,
为短轴的一个端点, ![]() 是椭圆
是椭圆![]() 上的一点,满足
上的一点,满足![]() ,且
,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,若
两点,若![]() 是以
是以![]() 为顶点的等腰三角形,求点
为顶点的等腰三角形,求点![]() 到直线
到直线![]() 距离的取值范围.
距离的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由已知![]() ,设
,设![]() ,则
,则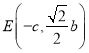 ,
, ![]() ,
, ![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程;(2)设点
的方程;(2)设点![]() ,(
,( ![]() ),直线
),直线![]() 的方程为
的方程为![]() ,k≠0,由
,k≠0,由![]() ,得:
,得: ![]() ,由此利用韦达定理、中点坐标公式、点到直线的距离公式,结合已知条件能求出点
,由此利用韦达定理、中点坐标公式、点到直线的距离公式,结合已知条件能求出点![]() 到直线距离的取值范围.
到直线距离的取值范围.
试题解析:(1)由已知![]() ,设
,设![]() ,即
,即![]()
∴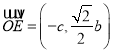 即
即 ∴
∴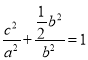 得:
得: ![]() ①
①
又![]() 的周长为
的周长为![]() ∴
∴ ![]() ②
②
又①②得: ![]() ∴
∴![]() ∴所求椭圆
∴所求椭圆![]() 的方程为:
的方程为: ![]()
(2)设点![]() ,直线
,直线![]() 的方程为
的方程为![]()
由![]() 消去
消去![]() ,得:
,得: ![]()
设![]() ,
, ![]() 中点为
中点为![]()
则![]() ∴
∴![]()
∴![]()
![]() 即
即
∵![]() 是以
是以![]() 为顶点的等腰三角形 ∴
为顶点的等腰三角形 ∴![]() 即
即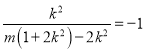
∴
设点![]() 到直线
到直线![]() 距离为
距离为![]() ,
,
则 ∴
∴![]()
即点![]() 到直线距离的取值范围是
到直线距离的取值范围是![]() 。
。

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】自驾游从![]() 地到
地到![]() 地有甲乙两条线路,甲线路是
地有甲乙两条线路,甲线路是![]() ,乙线是
,乙线是![]() ,其中
,其中![]() 段、
段、![]() 段、
段、![]() 段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率
段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率![]() 在
在![]() 上变化,
上变化, ![]() 在
在![]() 上变化.在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计
上变化.在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计![]() 段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
CD段 | EF段 | GH段 | |||
堵车概率 |
|
|
| ||
平均堵车时间 (单位:小时) |
| 2 | 1 | ||
(表1) | |||||
堵车时间(单位:小时) | 频数 | ||||
| 8 | ||||
| 6 | ||||
| 38 | ||||
| 24 | ||||
| 24 | ||||
(表2) | |||||
(1)求![]() 段平均堵车时间
段平均堵车时间![]() 的值.
的值.
(2)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
(3)在(2)的条件下,某4名司机中走甲线路的人数记为X,求X的数学期望。
【题目】从一批土鸡蛋中,随机抽取n个得到一个样本,其重量(单位:克)的频数分布表如表:
分组(重量) | [80,85) | [85,90) | [90,95) | [95,100] |
频数(个) | 10 | 50 | m | 15 |
已知从n个土鸡蛋中随机抽取一个,抽到重量在在[90,95)的土鸡蛋的根底为 ![]()
(1)求出n,m的值及该样本的众数;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的土鸡蛋中共抽取5个,再从这5个土鸡蛋中任取2 个,其重量分别是g1 , g2 , 求|g1﹣g2|≥10概率.