题目内容
函数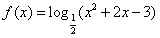 的递增区间是______.
的递增区间是______.
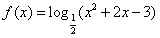 的递增区间是______.
的递增区间是______.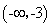
试题分析:根据题意,要使得原式有意义,则满足
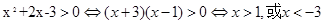 ,而结合已知外层是底数小于1的递减的对数函数,内层是二次函数,对称轴为x=-1,开口向上,则可知递增区间即为内层的减区间,即当x<-3时成立,故答案为
,而结合已知外层是底数小于1的递减的对数函数,内层是二次函数,对称轴为x=-1,开口向上,则可知递增区间即为内层的减区间,即当x<-3时成立,故答案为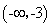 。
。点评:解题的关键是先确定定义域,然后内外结合,同增异减的思想来求解单调区间,属于基础题。

练习册系列答案
相关题目
题目内容
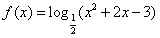 的递增区间是______.
的递增区间是______.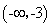
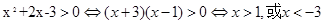 ,而结合已知外层是底数小于1的递减的对数函数,内层是二次函数,对称轴为x=-1,开口向上,则可知递增区间即为内层的减区间,即当x<-3时成立,故答案为
,而结合已知外层是底数小于1的递减的对数函数,内层是二次函数,对称轴为x=-1,开口向上,则可知递增区间即为内层的减区间,即当x<-3时成立,故答案为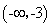 。
。