题目内容
若双曲线 上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
- A.
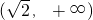
- B.

- C.
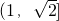
- D.
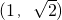
C
分析:由于双曲线得对称性,只讨论第一象限即可.根据双曲线方程,设其上一点P的坐标为P( ,btanθ),其中为θ锐角,求出直线OP方程:y=
,btanθ),其中为θ锐角,求出直线OP方程:y= x.设右焦点F(c,0)关于直线OP的对称点为Q(x1,y1),根据点关于直线对称的知识,列方程组并化简消去y1,可得
x.设右焦点F(c,0)关于直线OP的对称点为Q(x1,y1),根据点关于直线对称的知识,列方程组并化简消去y1,可得 .因为不存在点P使得对称点Q在y轴上,所以不存在θ,使x1=0满足该方程,讨论这个方程解的情况,得
.因为不存在点P使得对称点Q在y轴上,所以不存在θ,使x1=0满足该方程,讨论这个方程解的情况,得 ,可得c2≤2a2,离心率满足
,可得c2≤2a2,离心率满足 .得到正确答案.
.得到正确答案.
解答:由于双曲线得对称性,只讨论第一象限即可.
设双曲线位于第一象限内一点P的坐标为( ,btanθ),其中为θ锐角,
,btanθ),其中为θ锐角,
∴直线OP的斜率为k= =
= ,可得直线OP方程为y=
,可得直线OP方程为y= x,
x,
设右焦点F(c,0)关于直线OP的对称点为Q(x1,y1),
∴ ,消去y1得:
,消去y1得: …(*),
…(*),
接下来讨论方程(*)的根的问题,
当x1=0时, ,将此方程进行变量分离,得:
,将此方程进行变量分离,得:
∵0<sin2θ<1
∴
而根据题意,不存在点P使得对称点Q在y轴上,所以不存在θ,使x1=0满足(*)式成立.
综上所述,可得 ,即
,即 ,可得c2≤2a2,离心率
,可得c2≤2a2,离心率
∵双曲线中,c>a
∴离心率e>1,可得 .
.
故选C
点评:本题给出双曲线上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,求双曲线离心率的取值范围,着重考查了双曲线的简单性质和点关于直线对称等知识点,属于中档题.
分析:由于双曲线得对称性,只讨论第一象限即可.根据双曲线方程,设其上一点P的坐标为P(
 ,btanθ),其中为θ锐角,求出直线OP方程:y=
,btanθ),其中为θ锐角,求出直线OP方程:y= x.设右焦点F(c,0)关于直线OP的对称点为Q(x1,y1),根据点关于直线对称的知识,列方程组并化简消去y1,可得
x.设右焦点F(c,0)关于直线OP的对称点为Q(x1,y1),根据点关于直线对称的知识,列方程组并化简消去y1,可得 .因为不存在点P使得对称点Q在y轴上,所以不存在θ,使x1=0满足该方程,讨论这个方程解的情况,得
.因为不存在点P使得对称点Q在y轴上,所以不存在θ,使x1=0满足该方程,讨论这个方程解的情况,得 ,可得c2≤2a2,离心率满足
,可得c2≤2a2,离心率满足 .得到正确答案.
.得到正确答案.解答:由于双曲线得对称性,只讨论第一象限即可.
设双曲线位于第一象限内一点P的坐标为(
 ,btanθ),其中为θ锐角,
,btanθ),其中为θ锐角,∴直线OP的斜率为k=
 =
= ,可得直线OP方程为y=
,可得直线OP方程为y= x,
x,设右焦点F(c,0)关于直线OP的对称点为Q(x1,y1),
∴
 ,消去y1得:
,消去y1得: …(*),
…(*),接下来讨论方程(*)的根的问题,
当x1=0时,
 ,将此方程进行变量分离,得:
,将此方程进行变量分离,得:
∵0<sin2θ<1
∴

而根据题意,不存在点P使得对称点Q在y轴上,所以不存在θ,使x1=0满足(*)式成立.
综上所述,可得
 ,即
,即 ,可得c2≤2a2,离心率
,可得c2≤2a2,离心率
∵双曲线中,c>a
∴离心率e>1,可得
 .
.故选C
点评:本题给出双曲线上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,求双曲线离心率的取值范围,着重考查了双曲线的简单性质和点关于直线对称等知识点,属于中档题.

练习册系列答案
相关题目
 上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为 B.
B. C.
C. D.
D.
 上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
( )
上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为
( ) B.
B. C.
C. D.
D.
 上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )


