题目内容
抛物线  的准线方程是( )
的准线方程是( )
| A.4 x + 1 = 0 | B.4 y + 1 =" 0" |
| C.2 x + 1 = 0 | D.2 y + 1 =" 0" |
B
解析试题分析:抛物线  焦点在y轴正半轴且2p=1,所以抛物线
焦点在y轴正半轴且2p=1,所以抛物线  的准线方程是
的准线方程是 ,即4 y + 1 = 0,故选B。
,即4 y + 1 = 0,故选B。
考点:本题主要考查抛物线标准方程及几何性质。
点评:简单题,确定抛物线的准线方程,应首先将抛物线方程化为标准形式,并注意四种不同情况。

练习册系列答案
相关题目
已知 ,
,  是椭圆
是椭圆 的两个焦点,点
的两个焦点,点 在此椭圆上且
在此椭圆上且 ,则
,则 的面积等于( )
的面积等于( )
A. | B. | C.2 | D. |
一动圆圆心在抛物线 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点
A.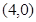 | B. | C. | D. |
下列曲线中,离心率为2的是( )
A. | B. | C. | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C.  | D. |
过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
焦点坐标是 ,
, ,且虚轴长为
,且虚轴长为 的双曲线的方程是( )
的双曲线的方程是( )
A. | B. |
C. | D. |
 +
+ =1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( ) ,
, ),P2的柱坐标是P2(2,
),P2的柱坐标是P2(2, ,1),则|P1P2|=( )
,1),则|P1P2|=( )