题目内容
函数
的单调递增区间是 （ ）
A． | B． |
C． | D． |
D
解析试题分析：根据题意，由于函数的单调递增区间即为函数
的单调减区间，即可知
,解得x的取值范围是，故可知函数递增区间为，选D.
考点：三角函数的单调性
点评：主要是考查了三角函数的单调性的运用，属于基础题。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知
，则角
= （ ）
A． | B． | C． | D． |
已知函数
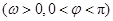的图象如图所示 ，则
等于（ ）
A． | B． | C． | D． |
如图所示是
的一部分，则其解析表达式为（ ）
A． |
B． |
C． |
D． |
关于函数
的四个结论：P1：最大值为
；P2：把函数
的图象向右平移
个单位后可得到函数
的图象； P3：单调递增区间为[
]，
； P4：图象的对称中心为(
)，．其中正确的结论有
| A．1个 | B．2个 | C．3个 | D．4个 |
＝( )
A． | B． | C． | D． |
关于函数
的四个结论：
P1：函数
的最大值为
；
P2：把函数
的图象向右平移
个单位后可得到函数的图象；
P3：函数的单调递增区间为[
]，
；
P4：函数图象的对称中心为(
)，．其中正确的结论有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
已知
，
，则
（ ）
A． | B． | C．- | D． |
已知
＝
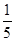，0<x<π，则tanx为
A．－ | B．－ | C．2 | D．－2 |