题目内容
甲、乙两名篮球运动员轮流投篮直至某人投中为止,计每次投篮甲投中的概率为0.4,乙投中的概率为0.6,而且不受其他投篮结果的影响.设甲投篮的次数为ξ,若甲先投,则P(ξ=k)等于( )
分析:由题意知甲和乙投篮不受其他投篮结果的影响,本题是一个相互独立事件同时发生的概率,甲投篮的次数为ξ,甲先投,则ξ=k表示甲第K次甲投中篮球,而乙前k-1次没有投中,甲k-1也没有投中,根据公式写出结果.
解答:解:∵甲和乙投篮不受其他投篮结果的影响,
∴本题是一个相互独立事件同时发生的概率,
∵每次投篮甲投中的概率为0.4,乙投中的概率为0.6,
甲投篮的次数为ξ,甲先投,则ξ=k表示甲第K次投中篮球,而乙前k-1次没有投中,
根据相互独立事件同时发生的概率得到0.4k-1×0.6k-1×0.4=0.24k-1×0.4;
故选B.
∴本题是一个相互独立事件同时发生的概率,
∵每次投篮甲投中的概率为0.4,乙投中的概率为0.6,
甲投篮的次数为ξ,甲先投,则ξ=k表示甲第K次投中篮球,而乙前k-1次没有投中,
根据相互独立事件同时发生的概率得到0.4k-1×0.6k-1×0.4=0.24k-1×0.4;
故选B.
点评:本题考查相互独立事件同时发生的概率,是一个基础题,本题最大的障碍是理解ξ=k的意义,相互独立事件是指,两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下: 2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是
2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是 某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的平均数分别为( )
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员得分的平均数分别为( )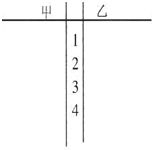 某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
 (2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )
(2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )