题目内容
如果tanαsinα<0,且0<sinα+cosα<1,那么α的终边在第
二
二
象限.分析:由条件求得 sinα>0,cosα<0,可得α的终边在第二象限,从而得出结论.
解答:解:由tanαsinα<0=
,可得cosα<0.
再由0<sinα+cosα<1,平方可得sinαcosα<0,
故有sinα>0,cosα<0,那么α的终边在第二象限,
故答案为 二.
| sin2α |
| cosα |
再由0<sinα+cosα<1,平方可得sinαcosα<0,
故有sinα>0,cosα<0,那么α的终边在第二象限,
故答案为 二.
点评:本题主要考查三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如果tanα=3,且sinα<0,那么cosα的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 =
= tan
tan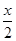 -
-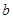 sin
sin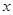 +4(其中
+4(其中
 0),如果
0),如果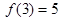 ,则
,则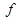 (2010
(2010 -3)的值为 ( )
-3)的值为 ( )