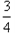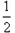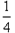题目内容
设椭圆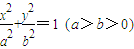 的中心、右焦点、右顶点依次分别为O、F、G,且直线
的中心、右焦点、右顶点依次分别为O、F、G,且直线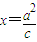 与x轴相交于点H,则
与x轴相交于点H,则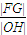 最大时椭圆的离心率为( )
最大时椭圆的离心率为( )A.2
B.

C.

D.

【答案】分析:先表示出 ,利用配方法,可求最值,从而可得结论.
,利用配方法,可求最值,从而可得结论.
解答:解:由题意, =
= =e-e2=
=e-e2=
∴ 时,
时, 取得最大值
取得最大值
故选C.
点评:本题考查椭圆的简单性质,考查配方法求函数的最值,属于基础题.
 ,利用配方法,可求最值,从而可得结论.
,利用配方法,可求最值,从而可得结论.解答:解:由题意,
 =
= =e-e2=
=e-e2=
∴
 时,
时, 取得最大值
取得最大值故选C.
点评:本题考查椭圆的简单性质,考查配方法求函数的最值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
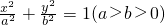 的中心、右焦点、右顶点依次分别为O、F、G,且直线
的中心、右焦点、右顶点依次分别为O、F、G,且直线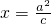 与x轴相交于点H,则
与x轴相交于点H,则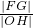 最大时椭圆的离心率为
最大时椭圆的离心率为


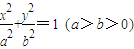 的中心、右焦点、右顶点依次分别为O、F、G,且直线
的中心、右焦点、右顶点依次分别为O、F、G,且直线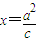 与x轴相交于点H,则
与x轴相交于点H,则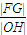 最大时椭圆的离心率为 .
最大时椭圆的离心率为 .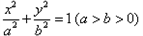 的中心、右焦点、右顶点依次分别为
的中心、右焦点、右顶点依次分别为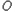 、
、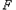 、
、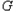 ,且直线
,且直线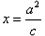 与
与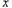 轴相交于点
轴相交于点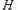 ,则
,则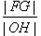 最大时椭圆的离心率为
最大时椭圆的离心率为