Question

已知函数f(x)=(x≠-1).设数列{a_n}满足a₁=1,a_n+1=f(a_n)，数列{b_n}满足b_n=|a_n-|,S_n=b₁+b₂+…+b_n(n∈N^*).

（1）用数学归纳法证明:b_n≤;

（2）证明:S_n＜.

Answer 1

证明：(1)当x≥0时,f(x)=1+≥1.因为a₁=1，所以a_n≥1(n∈N^*)

下面用数学归纳法证明不等式b_n≤.

（Ⅰ）当n=1时，b₁=-1，不等式成立，

（Ⅱ）假设当n=k时，不等式成立，即b_k≤.

那么b_k+1=|a_k+1-|=.

所以，当n=k+1时，不等式也成立.

根据（Ⅰ）和（Ⅱ），可知不等式对任意n∈N^*都成立.

（2）由（Ⅰ）知，b_n≤.所以

S_n=b₁+b₂+…+b_n≤(-1)+

=（-1）·.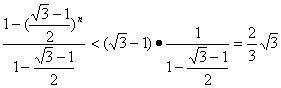

故对任意n∈N^*,S_n＜.