题目内容
定义在R上的函数f(x)满足 ,且函数
,且函数 为奇函数,给出下列命题:
为奇函数,给出下列命题:
(1)函数f(x)的周期为 ,
,
(2)函数f(x)关于点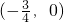 对称,
对称,
(3)函数f(x)关于y轴对称.其中正确的是______.
解:由题意定义在R上的函数y=f(x)满足条件  ,
,
故有 恒成立,故函数周期是3,
恒成立,故函数周期是3,
故(1)错;
又函数 是奇函数,其图象关于原点对称,
是奇函数,其图象关于原点对称,
而函数y=f(x)的图象可由函数 的图象向左平移
的图象向左平移 个单位得到,
个单位得到,
故函数y=f(x)的图象关于点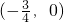 对称,
对称,
由此知(2)(3)是正确的选项,
故答案为:(2)(3)
分析:先由恒等式 得出函数的周期是T=3,可以判断(1)错,再由函数
得出函数的周期是T=3,可以判断(1)错,再由函数  是奇函数求出函数的对称点来判断(2)、(3);即可得答案.
是奇函数求出函数的对称点来判断(2)、(3);即可得答案.
点评:本小题主要考查函数奇偶性的性质、奇偶函数图象的对称性、函数的周期性等基础知识,考查数形结合思想、化归与转化思想.属于基础题.
 ,
,故有
 恒成立,故函数周期是3,
恒成立,故函数周期是3,故(1)错;
又函数
 是奇函数,其图象关于原点对称,
是奇函数,其图象关于原点对称,而函数y=f(x)的图象可由函数
 的图象向左平移
的图象向左平移 个单位得到,
个单位得到,故函数y=f(x)的图象关于点
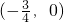 对称,
对称,由此知(2)(3)是正确的选项,
故答案为:(2)(3)
分析:先由恒等式
 得出函数的周期是T=3,可以判断(1)错,再由函数
得出函数的周期是T=3,可以判断(1)错,再由函数  是奇函数求出函数的对称点来判断(2)、(3);即可得答案.
是奇函数求出函数的对称点来判断(2)、(3);即可得答案.点评:本小题主要考查函数奇偶性的性质、奇偶函数图象的对称性、函数的周期性等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目