题目内容
(本小题满分12分)
如图,在三棱柱![]() 中,
中,![]() 平面
平面![]()
![]() 为
为![]() 的中点.
的中点.
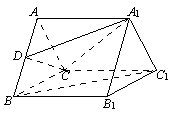 (1) 求证:
(1) 求证:![]() ∥平面
∥平面![]() ;
;
(2) 求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(方法一)⑴证明:如图一,连结![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .
.
在△![]() 中,
中,![]() 、
、![]() 为中点,∴
为中点,∴![]() ∥
∥![]() . (3分)
. (3分)
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() . (5分)
. (5分)
⑵解:二面角![]() 与二面角
与二面角![]() 互补.
互补.
如图二,作![]() ,垂足为
,垂足为![]() ,
,
又平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
作![]()
![]()
![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,则
,则![]() ,
,
∴∠![]() 为二面角
为二面角![]() 的平面角. (8分)
的平面角. (8分)
设![]() ,
,
在等边△![]() 中,
中,![]() 为中点,∴
为中点,∴![]() ,在正方形
,在正方形![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.
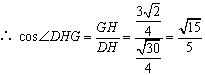 . (11分
. (11分
∴所求二面角的余弦值为![]() . (12分)
. (12分)
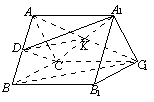
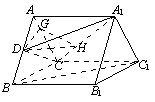
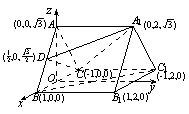
图一 图二 图三
(方法二)证明:如图三以![]() 的中点
的中点![]() 为原点建系,设
为原点建系,设![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则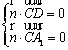 .又
.又![]() ,
,![]() ,
,
∴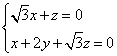 .令
.令![]() ,∴
,∴![]() . (3分)
. (3分)
∵![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() . (5分)
. (5分)
⑵解:设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则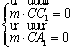 .又
.又![]() ,
,![]() ,
,
∴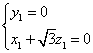 .令
.令![]() ,∴
,∴![]() . (8分)
. (8分)
∴![]() . (11分)
. (11分)
∴所求二面角的余弦值为![]() . (12分)
. (12分)

练习册系列答案
相关题目