题目内容
曲线f（x）=（x-3）ex，当x∈（2，+∞）时，f（x）＞k恒成立，则实数k的取值范围是______．
f′（x）=ex+（x-3）ex=ex（x-2），
当x∈（2，+∞）时，f′（x）＞0，
所以f（x）在（2，+∞）上单调递增，f（x）＞f（2）=-e2，
因为x∈（2，+∞）时，f（x）＞k恒成立，
所以-e2≥k，即实数k的取值范围是（-∞，-e2]．
故答案为：（-∞，-e2]．
当x∈（2，+∞）时，f′（x）＞0，
所以f（x）在（2，+∞）上单调递增，f（x）＞f（2）=-e2，
因为x∈（2，+∞）时，f（x）＞k恒成立，
所以-e2≥k，即实数k的取值范围是（-∞，-e2]．
故答案为：（-∞，-e2]．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
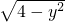，存在自公切线的是
，存在自公切线的是（ ）
，存在自公切线的是（ ）