题目内容
设a1=2，
，
，n∈N*，则b2011= ．
【答案】分析：先确定{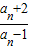
}是以4为首项，-2为公比的等比数列，求出其通项，即可求得b2011的值．
解答：解：∵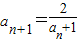
，∴
=
∴
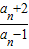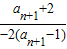
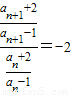
∵a1=2，∴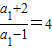
∴{
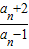}是以4为首项，-2为公比的等比数列
∴
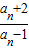=4×（-2）n-1
∴b2011=|4×（-2）2010|-1=22012-1
故答案为：22012-1
点评：本题考查归纳推理，考查等比数列的定义与通项，确定数列为等比数列是解题的关键．
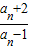}是以4为首项，-2为公比的等比数列，求出其通项，即可求得b2011的值．解答：解：∵
，∴=∴
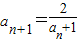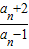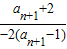
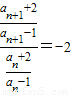
∵a1=2，∴
∴{
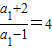
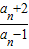}是以4为首项，-2为公比的等比数列∴
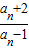=4×（-2）n-1∴b2011=|4×（-2）2010|-1=22012-1
故答案为：22012-1
点评：本题考查归纳推理，考查等比数列的定义与通项，确定数列为等比数列是解题的关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
，
，n∈N*，则b2011=________．