题目内容
【题目】已知f(ex)=ax2﹣x,a∈R.
(1)求f(x)的解析式;
(2)求x∈(0,1]时,f(x)的值域;
(3)设a>0,若h(x)=[f(x)+1﹣a]logxe对任意的x1 , x2∈[e﹣3 , e﹣1],总有|h(x1)﹣h(x2)|≤a+ ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】
(1)解:设ex=t,则x=lnt>0,所以f(t)=a(lnt)2﹣lnt
所以f(x)=a(lnx)2﹣lnx(x>0)
(2)解:设lnx=m(m≤0),则f(x)=g(m)=am2﹣m
当a=0时,f(x)=g(m)=﹣m,g(m)的值域为[0,+∞)
当a≠0时, ![]()
若a>0, ![]() ,g(m)的值域为[0,+∞)
,g(m)的值域为[0,+∞)
若a<0, ![]() ,g(m)在
,g(m)在 ![]() 上单调递增,在
上单调递增,在 ![]() 上单调递减,g(m)的值域为
上单调递减,g(m)的值域为 ![]() )
)
综上,当a≥0时f(x)的值域为[0,+∞)
当a<0时f(x)的值域为 ![]()
(3)解:因为 ![]() 对任意
对任意 ![]() 总有
总有 ![]()
所以h(x)在[e﹣3,e﹣1]满足 ![]()
设lnx=s(s∈[﹣3,﹣1]),则 ![]() ,s∈[﹣3,﹣1]
,s∈[﹣3,﹣1]
当1﹣a<0即a>1时r(s)在区间[﹣3,﹣1]单调递增
所以 ![]() ,即
,即 ![]() ,所以
,所以 ![]() (舍)
(舍)
当a=1时,r(s)=s﹣1,不符合题意
当0<a<1时,则 ![]() =a(s+
=a(s+ ![]() )﹣1,s∈[﹣3,﹣1]
)﹣1,s∈[﹣3,﹣1]
若 ![]() 即
即 ![]() 时,r(s)在区间[﹣3,﹣1]单调递增
时,r(s)在区间[﹣3,﹣1]单调递增
所以 ![]() ,则
,则 ![]()
若 ![]() 即
即 ![]() 时r(s)在
时r(s)在 ![]() 递增,在
递增,在 ![]() 递减
递减
所以 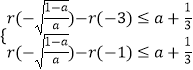 ,得
,得 ![]()
若 ![]() 即
即 ![]() 时r(s)在区间[﹣3,﹣1]单调递减
时r(s)在区间[﹣3,﹣1]单调递减
所以 ![]() ,即
,即 ![]() ,得
,得 ![]()
综上所述: ![]()
【解析】(1)利用换元法进行求解即可.(2)根据函数的解析式即可求函数的值域.(3)根据函数恒成立问题,建立不等式关系进行求解即可.
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,以及对二次函数的性质的理解,了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.