题目内容
已知f(x)=x2-ax,x∈[1,+∞).
(1)求f(x)的最小值g(a);
(2)求函数h(a)=g(a)-a2的最大值;
(3)写出函数h(a)的单调减区间.
解: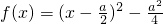
(1)当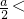 1时,函数在[1,+∞)上单调增,∴f(x)的最小值g(a)=f(1)=1-a;
1时,函数在[1,+∞)上单调增,∴f(x)的最小值g(a)=f(1)=1-a;
当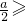 1时,f(x)的最小值g(a)=
1时,f(x)的最小值g(a)=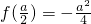
综上知,f(x)的最小值g(a)=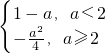 ;
;
(2)h(a)=g(a)-a2=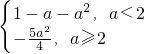
当a<2时,h(a)=1-a-a2=-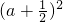 +
+ ≤
≤ ;
;
当a≥2时,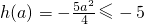
∴函数h(a)=g(a)-a2的最大值为 ;
;
(3)由(2)知,函数h(a)的单调减区间为[- ,+∞)
,+∞)
分析:(1)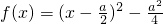 ,将函数的对称轴与区间联系起来,分类讨论,可求f(x)的最小值;
,将函数的对称轴与区间联系起来,分类讨论,可求f(x)的最小值;
(2)h(a)=g(a)-a2=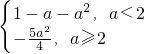 ,分段求出函数的最大值,比较即可得到函数h(a)=g(a)-a2的最大值;
,分段求出函数的最大值,比较即可得到函数h(a)=g(a)-a2的最大值;
(3)由(2)可确定函数h(a)的单调减区间.
点评:本题考查二次函数的单调性与最值,考查分段函数,解题的关键是确定函数的解析式,属于中档题.
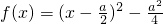
(1)当
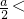 1时,函数在[1,+∞)上单调增,∴f(x)的最小值g(a)=f(1)=1-a;
1时,函数在[1,+∞)上单调增,∴f(x)的最小值g(a)=f(1)=1-a;当
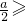 1时,f(x)的最小值g(a)=
1时,f(x)的最小值g(a)=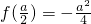
综上知,f(x)的最小值g(a)=
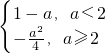 ;
;(2)h(a)=g(a)-a2=
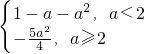
当a<2时,h(a)=1-a-a2=-
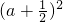 +
+ ≤
≤ ;
;当a≥2时,
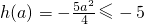
∴函数h(a)=g(a)-a2的最大值为
 ;
;(3)由(2)知,函数h(a)的单调减区间为[-
 ,+∞)
,+∞)分析:(1)
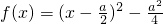 ,将函数的对称轴与区间联系起来,分类讨论,可求f(x)的最小值;
,将函数的对称轴与区间联系起来,分类讨论,可求f(x)的最小值;(2)h(a)=g(a)-a2=
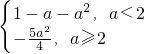 ,分段求出函数的最大值,比较即可得到函数h(a)=g(a)-a2的最大值;
,分段求出函数的最大值,比较即可得到函数h(a)=g(a)-a2的最大值;(3)由(2)可确定函数h(a)的单调减区间.
点评:本题考查二次函数的单调性与最值,考查分段函数,解题的关键是确定函数的解析式,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目