题目内容
对于
，有如下四个命题:
①若
，则
为等腰三角形；②若
，则是不一定直角三角形；③若
，则是钝角三角形④若
，则是等边三角形.其中正确的命题是 .
④.
解析试题分析：对于命题①，若
，则
，所以
，所以
，故也可能是直角三角形，故命题①为假命题；对于命题②，取
，
，则
，此时为钝角三角形，故不一定是直角三角形，故命题②为真命题；对于命题③，由于
，所以
，故有
，故角
为锐角，并不能说明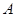
、
其中一个为钝角，即不一定是钝角三角形，所以命题③为假命题；对于命题④，由于，所以
，于是得到
，由于
，所以
，同理可得
，
，由于函数
在
上是单调递增的，故
，于是有
，所以为等边三角形.故正确的命题为②④.
考点：1.诱导公式；2.正弦定理；3.余弦定理
练习册系列答案
相关题目
是定义在区间
上的奇函数，令
，并有关于函数
的四个论断：
，对于
内的任意实数
，
恒成立；
；
，
有两个零点；
，则方程
必有3个实数根；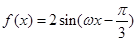
（
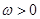）的图象向左平移
个单位，得到函数
的图象，若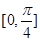
上为增函数，则
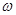的最大值为 ．
，则
= .
，
，
，则
的值=________________.
，三等分单位圆时，有相应正确关系为
，由此推出：四等分单位圆时的相应正确关系为 .
是偶函数，
，则
.
的图象关于直线
对称，则
的单调递增区间为 ．
，
，
在
上的部分图象如图所示，则
的值为 ．