题目内容
【题目】对点
的直线l分別交
与
于
两点.
(1)设
的面积为
，求直线l的方程；
(2)当
最小时，求直线l的方程.
【答案】(1)
；
(2)
.
【解析】
(1)设所求直线l的方程,分别与直线
与
联立，得出交点A、B的纵坐标，根据三角形的面积公式得出方程，求解可得所求直线的方程；
(2)设直线l的参数式方程，分别代入直线与中，得出
、
，从而得出
，运用三角函数的恒等变形得出其最小值，由（1）得出交点的纵坐标可求解出满足题意的值，得出直线的方程.
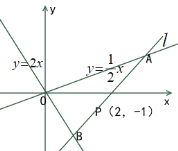
（1）设
，直线
，
由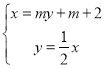
化简得A点的纵坐标
，
由
，化简得B点的纵坐标
，
所以，
，化简得
，
故直线
的方程为：；
（2）设直线的倾斜角为
,所以直线的参数方程为:
（
为参数），
将直线的参数方程分别代入 与得：
，
所以
，
由（1）得
，
，
当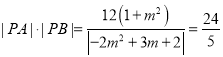
时，化简得
或
，解得
或
.
因为点A在第一象限，所以
，所以
，所以，
所以直线
.
故得解.
【题目】（本小题满分13分） 已知双曲线
的两个焦点为
的曲线C上.
（Ⅰ）求双曲线C的方程；
（Ⅱ）记O为坐标原点，过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为
求直线l的方程
【题目】物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性，对某公司的该产品的销量与价格进行了统计分析，得到如下数据和散点图：
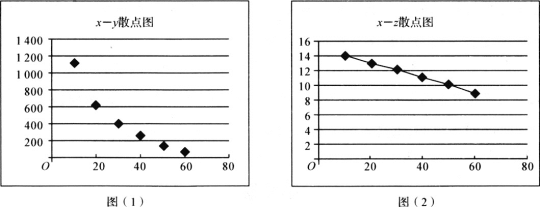
定价x（元／kg） | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y（kg） | 1150 | 643 | 424 | 262 | 165 | 86 |
z＝21ny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
（参考数据：
，
，
，
）
（Ⅰ）根据散点图判断，y与x和z与x哪一对具有的线性相关性较强（给出判断即可，不必说明理由）？
（Ⅱ）根据（Ⅰ）的判断结果及数据，建立y关于x的回归方程（方程中的系数均保留两位有效数字）．
附：对于一组数据（x1，y1），（x2，y2），（x3，y3），…，（xn，yn），其回归直线
的斜率和截距的最小二乘估计分别为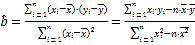
，
．
