Question

已知抛物线C：x²=4y，直线y=kx-1与C交于第一象限的两点A、B，F是C的焦点，且|AF|=3|FB|，则k=（　　）

• A．

  3

  ?
• B．

  3

  3

• C．

  3

  2

• D．

  2 3

  3

Answer 1

分析：根据直线方程可知直线恒过定点C（0，-1），如图过A、B分别作BQ⊥l于Q，AP⊥l于P，由|AF|=3|FB|，则|AP|=3|BQ|，进而推断出|BE|=|BF|，进而求得点B的纵坐标，则点B的坐标可得，最后利用直线上的两点求得直线的斜率．

解答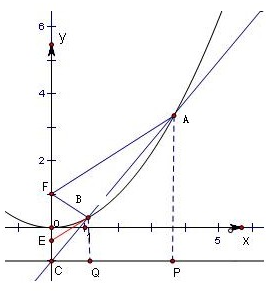：解：设抛物线C：x²=4y的准线为l：y=-1，
直线y=kx-1（k＞0）恒过定点C（0，-1）
如图过A、B分别作AP⊥l于P，BQ⊥l于Q，
由|AF|=3|FB|，则|AP|=3|BQ|，
点B为AC的一个三等份点，取CF的一个三等份点E（0，-

1

3

），连接BE，
则|BE|=

1

3

|AF|，
∴|BE|=|BF|，点B的纵坐标为

1

3

，
故点B的坐标为（

2 3

3

，

1

3

）
∴k=

1 3 -(-1)

2 2 3 -0

=

2 3

3

．
故选D．

点评：本题主要考查了抛物线的简单性质，考查了对抛物线的基础知识的灵活运用，考查了数形结合的思想．