题目内容
(14分)已知数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, ,
,
(1)设 ,数列
,数列 为等比数列,求实数
为等比数列,求实数 的值;
的值;
(2)设 ,求数列
,求数列 的通项公式;
的通项公式;
(3)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
(1) ;(2)
;(2) ;(3)
;(3)
解析试题分析:(1)由 ,得
,得 ,
,
所以 ,
,
所以数列{ }为等比数列,又因为
}为等比数列,又因为 ,数列
,数列 为等比数列,
为等比数列,
所以 .
.
(2)由(1)知
所以 ,
,
所以 为等差数列,
为等差数列, ,
,
(3) 由(2)知 ,
, ,
,
所以 .
.
考点:等比数列的定义,等差数列的定义,数列求和.
点评:解本小题关键是利用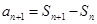 ,得到
,得到 ,
,
从而得到{ }为等比数列,因而
}为等比数列,因而 ,数列
,数列 为等比数列,可确定
为等比数列,可确定 .
.
(2)再(1)的基础上,可求出 ,从而确定
,从而确定 为等差数列,问题得解.
为等差数列,问题得解.
(3)求出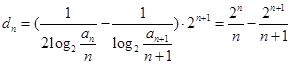 是解本小题的关键,显然再采用叠加相消求和即可.
是解本小题的关键,显然再采用叠加相消求和即可.

练习册系列答案
相关题目
设a、b、c均为正实数,则三个数a+ 、b+
、b+ 、c+
、c+ ( ).
( ).
| A.都大于2 | B.都小于2 |
| C.至少有一个不大于2 | D.至少有一个不小于2 |
 中,已知
中,已知 .
.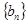 是等差数列;
是等差数列; 满足
满足 ,求
,求 .
. 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
. 的值,并求数列
的值,并求数列 为数列
为数列 的前
的前 满足
满足 ,
, ,求数列
,求数列 的通项公式.
的通项公式. 的前n项和,求Tn.
的前n项和,求Tn. 的前
的前 项和为
项和为 ,对一切正整数,点
,对一切正整数,点 都在函数
都在函数 的图像上.
的图像上. ,求数列
,求数列 的前项和
的前项和 .
. 的前
的前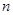 项和
项和 。(1)求数列
。(1)求数列 ,且数列
,且数列 的前
的前 。若
。若 ,求
,求 中,
中, .
. 的顺序,使它成为等比数列
的顺序,使它成为等比数列 的前三项,求
的前三项,求 项和.
项和.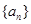 的前
的前 项和为
项和为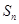 ,且满足
,且满足 (
( 满足
满足 ,且
,且 ,求数列
,求数列