题目内容
过点
作一直线
，使它被两直线
和
所截的线段
以
为中点，求此直线
的方程．
.
解析试题分析：根据题意，需对的斜率
是否存在分类讨论：若不存在，则：
不合题意，若存在，则可设直线：
，联立方程组即可求得与
，
的交点分别为
，
，再由
中点为即可得到关于的方程
.
试题解析：（1）当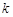
不存在时，：不满足题意； 2分
（2）当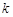存在时，设直线：， 1分
可得，， 6分
由中点坐标公式得
2分
∴直线方程为. 1分
考点：1.直线的方程；2.中点坐标公式.
练习册系列答案
应用题作业本系列答案
相关题目
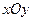中, 二元一次方程
(
不同时为
)表示过原点的直线. 类比以上结论有: 在空间直角坐标系
中, 三元一次方程
（
不同时为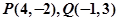
两点，且在
轴上截得的线段长为
，半径小于5.（1）求直线
与圆C的方程；（2）若直线
，直线
与圆C交于点A、B，且以AB为直径的圆经过坐标原点，求直线
与圆
相切的直线方程为 ．
，过左焦点F1作x轴的垂线交椭圆于A、A′两点，|AA′|=4．
