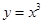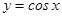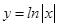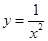题目内容
设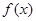 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当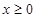 时,
时,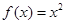 ,若对任意的
,若对任意的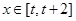 ,不等式
,不等式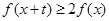 恒成立,则实数
恒成立,则实数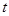 的取值范围是( )
的取值范围是( )
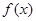 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当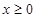 时,
时,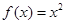 ,若对任意的
,若对任意的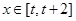 ,不等式
,不等式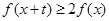 恒成立,则实数
恒成立,则实数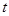 的取值范围是( )
的取值范围是( )A.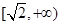 | B.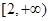 |
C.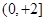 | D.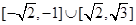 |
A
试题分析:因为
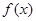 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当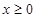 时,
时,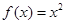 ,所以
,所以 时,
时, ,所以
,所以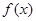 在R上单调递增,且
在R上单调递增,且 。对任意的
。对任意的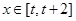 ,不等式
,不等式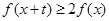 恒成立,即
恒成立,即 恒成立。因为
恒成立。因为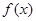 在R上单调递增,所以任意的
在R上单调递增,所以任意的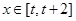 ,
, 恒成立。即
恒成立。即 恒成立,当
恒成立,当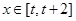 时,
时, ,所以只需
,所以只需 ,解得
,解得 。故A正确。
。故A正确。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
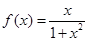 是定义在
是定义在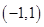 上的函数
上的函数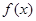 的奇偶性;
的奇偶性;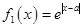 ,
,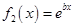 .
.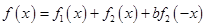 ,是否存在
,是否存在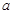 、
、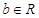 ,使
,使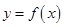 为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;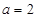 ,
,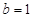 ,求
,求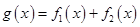 在
在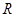 上的单调区间;
上的单调区间;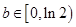 ,
,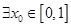 对
对 ,,有
,,有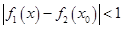 成立,求
成立,求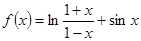 ,则关于
,则关于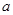 的不等式
的不等式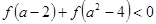 的解集是_______.
的解集是_______.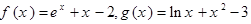 ,若实数
,若实数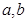 满足
满足 ,则( )
,则( )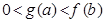
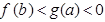
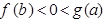
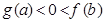
 是偶函数,且
是偶函数,且 上是增函数,如果
上是增函数,如果 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是( )
的取值范围是( )



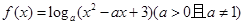 满足:对任意实数
满足:对任意实数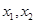 ,当
,当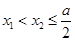 时,总有
时,总有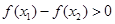 ,则实数
,则实数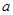 的取值范围是( )
的取值范围是( )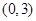
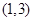
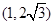
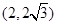
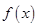 是
是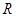 上的减函数,且
上的减函数,且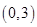 和
和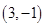 ,则不等式
,则不等式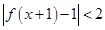 的解集是( )
的解集是( )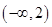
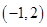
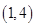
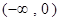 上单调递增的是 ( )
上单调递增的是 ( )