题目内容
若an=
(n∈N*),则
an=
|
| lim |
| n→+∞ |
0
0
.分析:当n→∞时,an=
,所以问题转化为求
,进而可以得解.
| 1 |
| 2n-6 |
| lim |
| n→+∞ |
| 1 |
| 2n-6 |
解答:解:由题意,n→+∞时,an=
,∴2n-6→+∞,
∴an=
→0
即
an=0
故答案为0
| 1 |
| 2n-6 |
∴an=
| 1 |
| 2n-6 |
即
| lim |
| n→+∞ |
故答案为0
点评:本题的考点是数列的极限,主要考查分段函数的极限,关键是转化为求
,进而可以得解.
| lim |
| n→+∞ |
| 1 |
| 2n-6 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
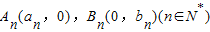 ,其中数列{an},{bn}都是递增数列.
,其中数列{an},{bn}都是递增数列.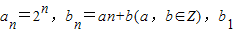 ≥-12,记直线AnBn的斜率为kn,数列{kn}的前8项依次递减,求满足条件的数列{bn}的个数.
≥-12,记直线AnBn的斜率为kn,数列{kn}的前8项依次递减,求满足条件的数列{bn}的个数.