题目内容
已知向量
，向量
，函数
小题1:若
且当
时，求函数
的单调递减区间；
小题2:当
时，写出由函数
的图象变换到函数
的图象的变换过程.
，向量，函数小题1:若且当时，求函数的单调递减区间；小题2:当
时，写出由函数的图象变换到函数的图象的变换过程.小题1:当
时，的单调递减区间为
同理，当
时，的单调递减区间为
小题2:1°将
的图象向右平移
个单位可得函数
的图象。2°将所得函数图象上每个点的纵坐标扩大为原来的
倍，而横坐标保持不变，可得函数
的图象.3°再将所得图象向上平移一个单位，可得
的图象.小题1:
当
时，由
得单调递减区间为同理，当
时，函数的单调递减区间为小题2:当
，变换过程如下：1°将
的图象向右平移个单位可得函数的图象。2°将所得函数图象上每个点的纵坐标扩大为原来的
倍，而横坐标保持不变，可得函数的图象.3°再将所得图象向上平移一个单位，可得
的图象.
练习册系列答案
相关题目
的最小正周期为
，其中
，则
= ．
（米）随着时间
而周期性变化，每天各时刻
的浪高数据的平均值如下表：
中选择一个合适的函数模型，并求出该拟合模型的解析式；
（其中
）的图象与x轴在原点右侧的第一个交点为N（6，0），又
（1）求这个函数解析式（2）设关于x的方程
在[0，8]内有两个不同根
，求
的值及k的取值范围。
的最小正周期和最大值分别为 ．
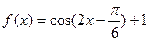的图象上所有的点的横坐标扩大为原来的2倍（纵坐标不变），得到
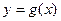的图象，再将
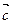平移，得到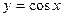
的图象，则
，1）
，-1）
x+
)+bcos(
),其中a,b,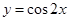 
的图象，只需将函数
的图象（ ）
B、向右平移
D、向右平移