题目内容
|
(本小题满分14分)
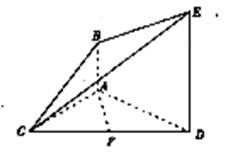
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,
AD=DE=2AB,且F是CD的中点。
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
|
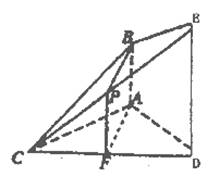
∵F为CD的中点,
∴FP//DE,且FP=![]()
又AB//DE,且AB=![]() W ww.k s5 u.co m
W ww.k s5 u.co m
∴AB//FP,且AB=FP,
∴ABPF为平行四边形,∴AF//BP。…………4分
又∵AF![]() 平面BCE,BP
平面BCE,BP![]() 平面BCE,
平面BCE,
∴AF//平面BCE。 …………6分
(II)∵△ACD为正三角形,∴AF⊥CD。
∵AB⊥平面ACD,DE//AB,
∴DE⊥平面ACD,又AF![]() 平面ACD,
平面ACD,
∴DE⊥AF。又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE。 …………14分
又BP//AF,∴BP⊥平面CDE。又∵BP![]() 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE。 …………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的外接圆,D
的外接圆,D =DE·DB;
=DE·DB; ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径 .
.
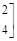 ,向量
,向量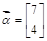 .
.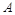 的特征值
的特征值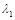 、
、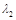 和特征向量
和特征向量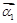 、
、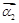 ;
;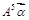 的值.
的值.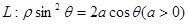 外的一点
外的一点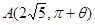 (其中
(其中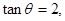
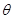 为锐角)作平行于
为锐角)作平行于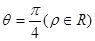 的直线
的直线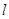 与曲线分别交于
与曲线分别交于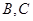 .
.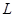 和直线
和直线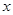 轴的正半轴建系);
轴的正半轴建系); 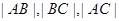 成等比数列,求
成等比数列,求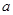 的值.
的值.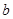 、
、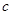 满足条件
满足条件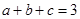 ,
,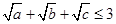 ;
;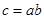 ,求
,求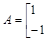
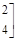 ,向量
,向量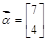 .
.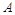 的特征值
的特征值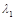 、
、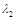 和特征向量
和特征向量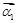 、
、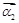 ;
;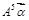 的值.
的值.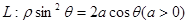 外的一点
外的一点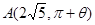 (其中
(其中
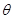 为锐角)作平行于
为锐角)作平行于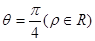 的直线
的直线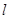 与曲线分别交于
与曲线分别交于 .
. 和直线
和直线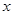 轴的正半轴建系);
轴的正半轴建系); 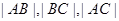 成等比数列,求
成等比数列,求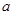 的值.
的值.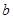 、
、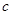 满足条件
满足条件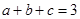 ,
,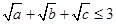 ;
; ,求
,求