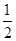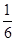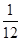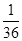题目内容
袋中装有大小相同的黑球和白球共 个,从中任取
个,从中任取 个都是白球的概率为
个都是白球的概率为 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取 个球,取出的球不放回,直到其中有一人取到白球时终止.用
个球,取出的球不放回,直到其中有一人取到白球时终止.用 表示取球终止时取球的总次数.
表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量 的概率分布及数学期望
的概率分布及数学期望 .
.
 个,从中任取
个,从中任取 个都是白球的概率为
个都是白球的概率为 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取 个球,取出的球不放回,直到其中有一人取到白球时终止.用
个球,取出的球不放回,直到其中有一人取到白球时终止.用 表示取球终止时取球的总次数.
表示取球终止时取球的总次数.(1)求袋中原有白球的个数;
(2)求随机变量
 的概率分布及数学期望
的概率分布及数学期望 .
.(1)袋中原有白球的个数为 .
.
(2)取球次数 的概率分布列为:
的概率分布列为:
数学期望为 .
.
 .
. (2)取球次数
 的概率分布列为:
的概率分布列为: |  |  |  |  |
 |  |  |  |  |
 .
. 试题分析:(1)设袋中原有
 个白球,可得方程
个白球,可得方程 ,解得
,解得 .
.(2)由题意,
 的可能取值为
的可能取值为 .
.由古典概型概率的计算公式,计算可得分布列为:
 |  |  |  |  |
 |  |  |  |  |
试题解析:(1)设袋中原有
 个白球,则从
个白球,则从 个球中任取
个球中任取 个球都是白球的概率为
个球都是白球的概率为 2分
2分由题意知
 ,化简得
,化简得 .
.解得
 或
或 (舍去) 5分
(舍去) 5分故袋中原有白球的个数为
 6分
6分(2)由题意,
 的可能取值为
的可能取值为 .
. ;
; ;
; ;
; .
. 所以取球次数
 的概率分布列为:
的概率分布列为: |  |  |  |  |
 |  |  |  |  |
所求数学期望为
 12分
12分
练习册系列答案
相关题目
 的分布列和数学期望
的分布列和数学期望 禽流感防御宣传工作,则在选出的宣传者中男、女都有的概率为( ).
禽流感防御宣传工作,则在选出的宣传者中男、女都有的概率为( ).