题目内容
如图，BA是⊙O的直径，AD是⊙O切线，C、E分别
为半圆上不同的两点，BC交AD于D，BE交AD于F。
（I） 求证：BE·BF=BC·BD。
（II） 若⊙O的半径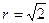
，BC=1，求AD。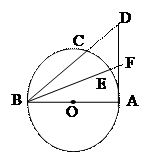
为半圆上不同的两点，BC交AD于D，BE交AD于F。
（I） 求证：BE·BF=BC·BD。
（II） 若⊙O的半径
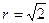，BC=1，求AD。（I）证明略
（II）
（II）
（1）证明连结AE 在△ABE和△ABF中∠AEB=∠BAF=90°
∠ABE=∠ABF
∴△ABE∽△ABF
∴
∴
——①
又连结AC在△ABC和△ABD中
同理可证△ABC∽△ABD
∴
∴
——②
由①②可知
∠ABE=∠ABF
∴△ABE∽△ABF
∴
∴——①又连结AC在△ABC和△ABD中
同理可证△ABC∽△ABD
∴
∴——②由①②可知
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
的切线方程是 （ ）
外一点p引切线与
；
。
，求
的值.
，∠OAP=30°，
则CP＝______.
，则以
为直径的圆标准方程是 ▲ ；
的半径和圆心坐标分别为
，半径为
，半径为
，则圆心C的极坐标为_______