题目内容
证明:函数f(x)=x+ (x>0)在区间(0,2)递减.
(x>0)在区间(0,2)递减.
证明:设x1、x2是区间,(0,2)上的任意两个数,且x1<x2,
∴f(x1)-f(x2)=(x1+ )-(x2+
)-(x2+ )=(x1-x2)(1-
)=(x1-x2)(1- )=
)=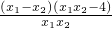
∵x1<x2,x1、x2∈(0,2)
∴x1-x2<0,0<x1x2<4,可得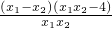 >0
>0
由此可得f(x1)>f(x2)
∴函数f(x)=x+ (x>0)在区间(0,2)上为减函数.
(x>0)在区间(0,2)上为减函数.
分析:设两个数x1、x2∈(0,2),且x1<x2,将f(x1)与f(x2)作差变形整理,再讨论得f(x1)>f(x2),由此即可得到f(x)=x+ 在区间(0,2)上为减函数.
在区间(0,2)上为减函数.
点评:本题通过证明一个函数在给定区间上为减函数,考查了用定义证明函数单调性的知识,属于基础题.
∴f(x1)-f(x2)=(x1+
 )-(x2+
)-(x2+ )=(x1-x2)(1-
)=(x1-x2)(1- )=
)=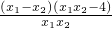
∵x1<x2,x1、x2∈(0,2)
∴x1-x2<0,0<x1x2<4,可得
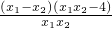 >0
>0由此可得f(x1)>f(x2)
∴函数f(x)=x+
 (x>0)在区间(0,2)上为减函数.
(x>0)在区间(0,2)上为减函数.分析:设两个数x1、x2∈(0,2),且x1<x2,将f(x1)与f(x2)作差变形整理,再讨论得f(x1)>f(x2),由此即可得到f(x)=x+
 在区间(0,2)上为减函数.
在区间(0,2)上为减函数.点评:本题通过证明一个函数在给定区间上为减函数,考查了用定义证明函数单调性的知识,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目