题目内容

设椭圆方程为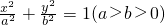 $数学公式$ ，PQ是过左焦点F且与x轴不垂直的弦，若在左准线l上存在点R，使△PQR为正三角形，则椭圆离心率e的取值范围是________．

$\text{[math]}$
分析：利用椭圆的定义，求出PQ的中点到准线的距离，再根据△PQR为正三角形，PQ是过左焦点F且与x轴不垂直的弦，构建不等式，即可求得椭圆离心率的范围．
解答：设弦PQ的中点为M，过点P、M、Q分别作准线l的垂线，垂足为P'、M'、Q'
则|MM'|= $\text{[math]}$ （|PP'|+|QQ'|）= $\text{[math]}$ （|PF|+|QF|）= $\text{[math]}$ |PQ|
假设存在点R，使△PQR为正三角形，则由|RM|= $\text{[math]}$ |PQ|，且|MM'|＜|RM|
得： $\text{[math]}$ |PQ|＜ $\text{[math]}$ |PQ|
∴ $\text{[math]}$ ＜ $\text{[math]}$
∴e＞ $\text{[math]}$
∴椭圆离心率e的取值范围是 $\text{[math]}$
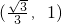
故答案为： $\text{[math]}$
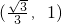
点评：本题考查椭圆的几何性质，考查椭圆的定义，考查解不等式，属于基础题．