题目内容
化简下列各式:(1)a2sin(-1 350°)+b2tan405°-(a-b)2cot765°-2abcos(-1 080°);
(2)sin(-![]() )+cos
)+cos![]() ·tan4π-
·tan4π-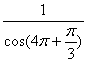 .
.
解析:(1)原式=a2sin(-4×360°+90°)+b2tan(360°+45°)-(a-b)2·cot(2×360°+45°)-2abcos(-3×360°)
=a2sin90°+b2tan45°-(a-b)2cot45°-2abcos0°
=a2+b2-(a-b)2-2ab=0.
(2)原式=sin(-2π+![]() )+cos
)+cos![]() ·tan0-
·tan0-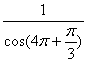 =sin
=sin![]() +0-
+0-![]() =
=![]() -2=-
-2=-![]() .
.
点评:公式一有两个作用:其一,可以把任意角的正弦、余弦、正切函数值分别化为0到2π(或0°到360°)角的同一三角函数值(其方法是先在[0,2π)范围内找出与它终边相同的角,再把它写成公式一的形式,然后得出结果);其二,便于研究这三种三角函数的性质.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 ;
; .
.