题目内容
已知实数x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则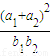 的取值范围是( )
的取值范围是( )A.[4,+∞)
B.(-∞,-4]∪[4,+∞)
C.(-∞,0]∪[4,+∞)
D.不能确定
【答案】分析:设x,a1,a2,y的公差为d,求出d= ,设x,b1,b2,y的公比为q,求出q=
,设x,b1,b2,y的公比为q,求出q= ,
, =
= .由此分类讨论可求出
.由此分类讨论可求出 的取值范围.
的取值范围.
解答:解:设x,a1,a2,y的公差为d,
则y=x+3d,∴d= ,
,
∴ ,
, .
.
设x,b1,b2,y的公比为q,
则y=xq3,∴q= ,
,
 ,
, ,
,
∴ =
= .
.
若x,y同号,则 =
= =
=
 .
.
若x>0,y<0,则 =
= ≤0.
≤0.
若x<0,y>0,则 =
= =-(-
=-(- )+2
)+2 .
.
综上所述, 的取值范围是(-∞,0]∪[4,+∞).
的取值范围是(-∞,0]∪[4,+∞).
故选C.
点评:本题考查数列的性质和应用,解题时要注意均值不等式的合理运用.
 ,设x,b1,b2,y的公比为q,求出q=
,设x,b1,b2,y的公比为q,求出q= ,
, =
= .由此分类讨论可求出
.由此分类讨论可求出 的取值范围.
的取值范围.解答:解:设x,a1,a2,y的公差为d,
则y=x+3d,∴d=
 ,
,∴
 ,
, .
.设x,b1,b2,y的公比为q,
则y=xq3,∴q=
 ,
, ,
, ,
,∴
 =
= .
.若x,y同号,则
 =
= =
=
 .
.若x>0,y<0,则
 =
= ≤0.
≤0.若x<0,y>0,则
 =
= =-(-
=-(- )+2
)+2 .
.综上所述,
 的取值范围是(-∞,0]∪[4,+∞).
的取值范围是(-∞,0]∪[4,+∞).故选C.
点评:本题考查数列的性质和应用,解题时要注意均值不等式的合理运用.

练习册系列答案
相关题目
已知实数x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则
的取值范围是( )
| (a1+a2)2 |
| b1b2 |
| A、[4,+∞) |
| B、(-∞,-4]∪[4,+∞) |
| C、(-∞,0]∪[4,+∞) |
| D、不能确定 |
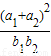 的取值范围是( )
的取值范围是( )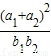 的取值范围是( )
的取值范围是( )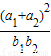 的取值范围是( )
的取值范围是( )