Question

（2011•许昌三模）已知O为平面直角坐标系的原点，F₂为双曲线

x2

a2

-

y2

b1

=1(a＞0，b＞0)的右焦点，E为OF₂的中点，过双曲线左顶点A作两渐近线的平行线分别与y轴交于C、D两点，B为双曲线的右顶点，若四边形ACBD的内切圆经过点E，则双曲线的离心率为（　　）

• A．2
• B．

  2

• C．

  3

• D．

  2 3

  3

Answer 1

分析：先根据双曲线的几何性质可推断出直线AD的方程，进而利用直线AD与四边形ACBD的内切圆相切，结合点到直线的距离公式得到a，b关系，最后求得a和c的关系式，即双曲线的离心率．

解答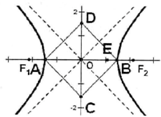：解：由题意得：直线AD的方程为：AD：y=

b

a

（x+a），
即：bx-ay+ab=0，
因为直线AD与四边形ACBD的内切圆相切，
故：r=d，即

c

2

=

ab

a2+b2

?a=b，
∴双曲线的离心率为e=

c

a

=

2

．
故选B．

点评：本题主要考查了双曲线的简单性质．涉及求双曲线的离心率问题，解题的关键是找到a，b和c的关系．