题目内容
已知数列{an}和{bn}满足a1=1且 .
.
(I)证明:数列{ }是等差数列,并求数列{an}的通项公式;
}是等差数列,并求数列{an}的通项公式;
(Ⅱ)求使不等式 对任意正整数n都成立的最大实数k.
对任意正整数n都成立的最大实数k.
(I)证明:∵数列{an}和{bn}满足a1=1,
且 ,
,
∴(1+2an)(1-2an+1)=1,
∴an-an+1=2an•an+1,
∴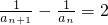 ,
,
∴数列 是以
是以 =1为首项,以2为公差的等差数列,
=1为首项,以2为公差的等差数列,
∴ =1+2(n-1)=2n-1,
=1+2(n-1)=2n-1,
∴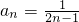 .
.
(Ⅱ)解:由(I)得 ,
,
 ,
,
 ,
,
则k ,
,
记f(n)= ,
,
则 ,
,
∴数列{f(n)}是递增数列,
要使原不等式对任意正整数n都成立,只要k≤f(1),
即 ,
,
∴满足条件的最大实数k为 .
.
分析:(I)由题设知(1+2an)(1-2an+1)=1,故an-an+1=2an•an+1,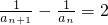 ,由此能够证明数列
,由此能够证明数列 是以
是以 =1为首项,以2为公差的等差数列,并能求出数列{an}的通项公式.
=1为首项,以2为公差的等差数列,并能求出数列{an}的通项公式.
(Ⅱ)由 ,知
,知 ,故
,故 ,则k
,则k ,由此能求出满足条件的最大实数k的值.
,由此能求出满足条件的最大实数k的值.
点评:本题考查数列与不等式的综合,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
且
 ,
,∴(1+2an)(1-2an+1)=1,
∴an-an+1=2an•an+1,
∴
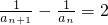 ,
,∴数列
 是以
是以 =1为首项,以2为公差的等差数列,
=1为首项,以2为公差的等差数列,∴
 =1+2(n-1)=2n-1,
=1+2(n-1)=2n-1,∴
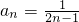 .
.(Ⅱ)解:由(I)得
 ,
, ,
, ,
,则k
 ,
,记f(n)=
 ,
,则
 ,
,∴数列{f(n)}是递增数列,
要使原不等式对任意正整数n都成立,只要k≤f(1),
即
 ,
,∴满足条件的最大实数k为
 .
.分析:(I)由题设知(1+2an)(1-2an+1)=1,故an-an+1=2an•an+1,
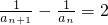 ,由此能够证明数列
,由此能够证明数列 是以
是以 =1为首项,以2为公差的等差数列,并能求出数列{an}的通项公式.
=1为首项,以2为公差的等差数列,并能求出数列{an}的通项公式.(Ⅱ)由
 ,知
,知 ,故
,故 ,则k
,则k ,由此能求出满足条件的最大实数k的值.
,由此能求出满足条件的最大实数k的值.点评:本题考查数列与不等式的综合,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目