题目内容
函数 ,数列
,数列 的前n项和
的前n项和 ,且
,且 同时满足:
同时满足:
① 不等式 ≤ 0的解集有且只有一个元素;
≤ 0的解集有且只有一个元素;
② 在定义域内存在 ,使得不等式
,使得不等式 成立.
成立.
(1) 求函数 的表达式;
的表达式;
(2) 求数列 的通项公式.
的通项公式.
(1)a=4,即
(2)
解析试题分析:解:(1)∵不等式f (x) ≤ 0的解集有且只有一个元素,∴ ,解得a=0或a=4.
,解得a=0或a=4.
当a=0时,函数 在(0,+∞)上递增,不满足条件②;
在(0,+∞)上递增,不满足条件②;
当a=4时,函数 在(0,2)上递减,满足条件②.
在(0,2)上递减,满足条件②.
综上得a=4,即 .
.
(2)由(1)知 ,
,
当n=1时, ; 当n ≥ 2时
; 当n ≥ 2时 
∴ 
考点:一元二次不等式,数列的通项公式
点评:主要是考查了二次不等式以及数列的通项公式与求和之间的关系的运用,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 .
. 的通项公式;
的通项公式; ,求证:
,求证: ;
; 的前
的前 .
. 的前n项和为
的前n项和为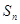 ,
,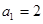 ,当n≥2时,
,当n≥2时, ,
, ,
, 成等差数列. (1)求数列
成等差数列. (1)求数列 的通项公式;
的通项公式; ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
.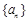 中,
中, ,
,
 且
且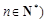 .
. ,
,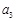 的值;
的值; 是等比数列,并求
是等比数列,并求 项和
项和 .
. 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前
的前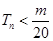 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 中,
中, ,且满足
,且满足
 .
. 及数列
及数列 求数列
求数列 的前
的前 项和
项和 .
. ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。 的前
的前 项和为
项和为 ,且
,且  N
N .
. 是三个互不相等的正整数,且
是三个互不相等的正整数,且 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.