题目内容
数列﹛an﹜的前n项和 Sn=n2an(n≥2).而a1=1,通过计算a2,a3,a4,猜想an=
- A.

- B.
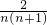
- C.

- D.

B
分析:利用数列﹛an﹜的前n项和 Sn=n2an(n≥2),a1=1,代入即可计算a2,a3,a4,从而可以猜想an.
解答:∵数列﹛an﹜的前n项和 Sn=n2an(n≥2),
∴S2=4a2,
∵a1=1
∴1+a2=4a2,
∴ ;
;
又S3=1+ +a3=9a3,
+a3=9a3,
∴
S4=1+ +
+ +a4=16a4
+a4=16a4
∴a4=
…
∴
故选B.
点评:本题以数列为载体,考查归纳推理,解题的关键是根据条件,求出前几项,并发现其规律.
分析:利用数列﹛an﹜的前n项和 Sn=n2an(n≥2),a1=1,代入即可计算a2,a3,a4,从而可以猜想an.
解答:∵数列﹛an﹜的前n项和 Sn=n2an(n≥2),
∴S2=4a2,
∵a1=1
∴1+a2=4a2,
∴
 ;
;又S3=1+
 +a3=9a3,
+a3=9a3,∴

S4=1+
 +
+ +a4=16a4
+a4=16a4∴a4=

…
∴

故选B.
点评:本题以数列为载体,考查归纳推理,解题的关键是根据条件,求出前几项,并发现其规律.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目