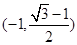题目内容
函数 的值域是
的值域是
- A.[-2,2]
- B.[
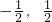 ]
] - C.[
 ]
] - D.[
 ]
]
C
分析:根据函数的几何意义,由圆心(0,0)到切线的距离等于半径可得 =1,解得k的值,即为所求.
=1,解得k的值,即为所求.
解答:函数 表示单位圆x2+y2=1上的点(cosx,sinx)与点(2,0)连线的斜率k.
表示单位圆x2+y2=1上的点(cosx,sinx)与点(2,0)连线的斜率k.
设过点(2,0)的与单位圆相切的切线方程为 y-0=k(x-2),即 kx-y-2k=0,
由圆心(0,0)到切线的距离等于半径可得 =1,解得 k=±
=1,解得 k=± ,
,
故k的范围为[ ],
],
即函数 的值域是[
的值域是[ ],
],
故选C.
点评:本题主要考查求函数的值域的方法,点到直线的距离公式的应用,明确函数的几何意义,是解题的关键,属于基础题.
分析:根据函数的几何意义,由圆心(0,0)到切线的距离等于半径可得
 =1,解得k的值,即为所求.
=1,解得k的值,即为所求.解答:函数
 表示单位圆x2+y2=1上的点(cosx,sinx)与点(2,0)连线的斜率k.
表示单位圆x2+y2=1上的点(cosx,sinx)与点(2,0)连线的斜率k.设过点(2,0)的与单位圆相切的切线方程为 y-0=k(x-2),即 kx-y-2k=0,
由圆心(0,0)到切线的距离等于半径可得
 =1,解得 k=±
=1,解得 k=± ,
,故k的范围为[
 ],
],即函数
 的值域是[
的值域是[ ],
],故选C.
点评:本题主要考查求函数的值域的方法,点到直线的距离公式的应用,明确函数的几何意义,是解题的关键,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 ,则函数
,则函数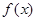 的值域是( ).
的值域是( ).  B.
B.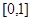 C.
C.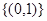 D.
D.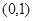
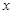 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数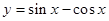 的值域是( )
的值域是( ) B.
B.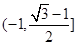 C.
C.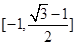 D.
D.