题目内容
13.已知指数函数f(x)=ax(a>0,且a≠1)的图象过点(-2,$\frac{9}{4}$),求函数的解析式.分析 根据指数函数的表达式,将已知点代入求出待定参数,求出指数函数的解析式即可.
解答 解:设指数函数为y=ax(a>0且a≠1)
将(-2,$\frac{9}{4}$),代入得 $\frac{9}{4}$=a-2解得a=$\frac{2}{3}$,所以y=${(\frac{2}{3})}^{x}$,
函数的解析式:f(x)=${(\frac{2}{3})}^{x}$.
点评 本题考查待定系数法求函数的解析式.若知函数模型求解析式时,常用此法.

练习册系列答案
相关题目
1.如图所示,圆O为正三角形ABC的内切圆,P为圆O上一点,向量$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y的取值范围为( )
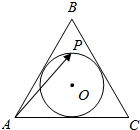

| A. | [$\frac{1}{2}$,1] | B. | [$\frac{1}{3}$,1] | C. | [$\frac{1}{4}$,1] | D. | [$\frac{1}{3}$,$\frac{1}{2}$] |
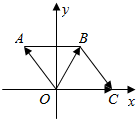 如图已知四边形AOCB中,|$\overrightarrow{OA}$|=5,$\overrightarrow{OC}$=(5,0),点B位于第一象限,若△BOC为正三角形.
如图已知四边形AOCB中,|$\overrightarrow{OA}$|=5,$\overrightarrow{OC}$=(5,0),点B位于第一象限,若△BOC为正三角形.