题目内容
已知函数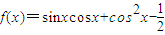
．（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求函数f（x）在
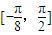的最大值和最小值．
【答案】分析：（Ⅰ）f（x）解析式利用二倍角的正弦、余弦函数公式化简后，再利用两角和与差的正弦函数公式化为一个角的正弦函数，找出ω的值，即可确定出函数的最小正周期；
（Ⅱ）由x的范围求出这个角的范围，利用正弦函数的图象与性质即可求出f（x）的最小值与最大值．
解答：解：（Ⅰ）由已知，得f（x）=
sin2x+
cos2x=
sin（2x+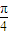
），
∵ω=2，∴T=π，
则f（x）的最小正周期为π；
（Ⅱ）∵-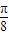
≤x≤
，∴0≤2x+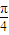
≤
，
则当2x+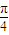
=
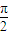时，即x=
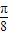时，f（x）取得最大值
；
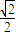当2x+
=
时，即x=
时，f（x）取得最小值-
．
点评：此题考查了二倍角的正弦、余弦函数公式，两角和与差的正弦函数公式，正弦函数的图象与性质，熟练掌握公式是解本题的关键．
（Ⅱ）由x的范围求出这个角的范围，利用正弦函数的图象与性质即可求出f（x）的最小值与最大值．
解答：解：（Ⅰ）由已知，得f（x）=
sin2x+cos2x=sin（2x+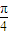），∵ω=2，∴T=π，
则f（x）的最小正周期为π；
（Ⅱ）∵-
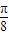≤x≤，∴0≤2x+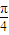≤，则当2x+
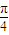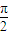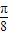=时，即x=时，f（x）取得最大值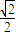；当2x+
=时，即x=时，f（x）取得最小值-．点评：此题考查了二倍角的正弦、余弦函数公式，两角和与差的正弦函数公式，正弦函数的图象与性质，熟练掌握公式是解本题的关键．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
．
．
个单位，得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．
．
上恒成立，求实数m的取值范围．
．
成等差数列，且
=9，求a的值．
．