题目内容
17.在平面直角坐标系xOy中,抛物线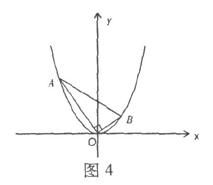
(Ⅰ)求![]() 的重心G(即三角形三条中线的交点)的轨迹方程;
的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
17.解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则
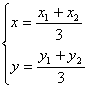 (1)
(1)
∵OA⊥OB ∴kOA·kOB=-1,即x1x2+y1y2=-1, (2)
又点A,B在抛物线上,有![]() ,代入(2)化简得x1x2=-1
,代入(2)化简得x1x2=-1
∴![]() 所以重心为G的轨迹方程为
所以重心为G的轨迹方程为![]()
(II)
![]()
由(I)得
![]() 当且仅当
当且仅当![]() 即x1=-x2=-1时,等号成立。
即x1=-x2=-1时,等号成立。
所以△AOB的面积存在最小值,存在时求最小值1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是