题目内容
(本题满分12分)已知函数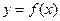
在定义域
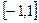上是奇函数，又是减函数。
（Ⅰ）证明：对任意的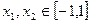
，有
（Ⅱ）解不等式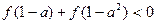
。
解：（Ⅰ）若
，显然不等式成立；
若
，
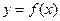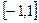在定义域上是奇函数，又是减函数，
故原不等式成立；
同理可证当
原不等式也成立。 ----6分
（Ⅱ）由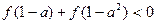和已知可得以下不等式组：
-----12分
解析
练习册系列答案
相关题目
题目内容
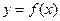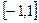(本题满分12分)已知函数在定义域上是奇函数，又是减函数。
（Ⅰ）证明：对任意的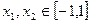，有
（Ⅱ）解不等式。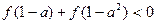
解：（Ⅰ）若，显然不等式成立；
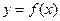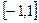若，在定义域上是奇函数，又是减函数，故原不等式成立；
同理可证当原不等式也成立。 ----6分
（Ⅱ）由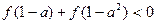和已知可得以下不等式组： -----12分
解析
，且
时，求证：
，使得函数
的定义域、值域都是
？若存在，则求出
的值，若不存在，请说明理由。
的值. 
的值.
的最小值不小于
, 且
.
的解析式;
的最小值为实数
的函数
，求函数
且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费.
对一切实数x,y都有
成立，且
.
的值 
，对任意的
，总存在
，使得
成立，求实数
的取值范围
的定义域为
,并满足(1)对于一切实数
，都有
；
； (3)
；
；
；
对任意的
恒成立，求实数
的取值范围。