题目内容
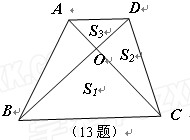
(本小题满分10分)如图,D、E分别是AB、AC边上的点,且不与顶点重合,已知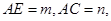
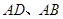 为方程
为方程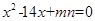 的两根
的两根
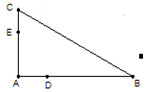
(1)证明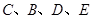 四点共圆
四点共圆
(2)若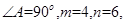 求
求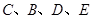 四点所在圆的半径
四点所在圆的半径
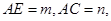
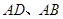 为方程
为方程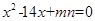 的两根
的两根
(1)证明
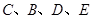 四点共圆
四点共圆(2)若
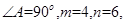 求
求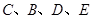 四点所在圆的半径
四点所在圆的半径(1)见解析;(2)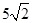
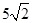
解:(Ⅰ)如图,连接DE,依题意在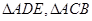 中,
中,
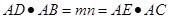 ,
,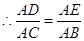 由因为
由因为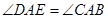 所以,
所以,
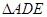 ∽
∽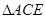 ,
,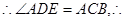 四点C、B、D、E共圆。
四点C、B、D、E共圆。
(Ⅱ)当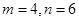 时,方程
时,方程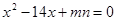 的根
的根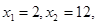
因而,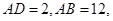 取CE中点G,BD中点F,分别过G,F 做AC,AB的垂线,两垂线交于点H,连接DH, 因为四点C、B、D、E共圆,所以,H为圆心,半径为DH.
取CE中点G,BD中点F,分别过G,F 做AC,AB的垂线,两垂线交于点H,连接DH, 因为四点C、B、D、E共圆,所以,H为圆心,半径为DH.
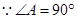 ,
,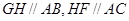 ,所以,
,所以,
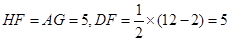 ,
,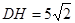
点评:此题考查平面几何中的圆与相似三角形及方程等概念和性质。注意把握判定与性质的作用。
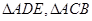 中,
中,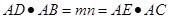 ,
,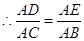 由因为
由因为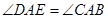 所以,
所以,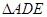 ∽
∽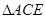 ,
,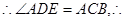 四点C、B、D、E共圆。
四点C、B、D、E共圆。(Ⅱ)当
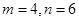 时,方程
时,方程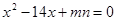 的根
的根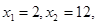
因而,
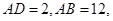 取CE中点G,BD中点F,分别过G,F 做AC,AB的垂线,两垂线交于点H,连接DH, 因为四点C、B、D、E共圆,所以,H为圆心,半径为DH.
取CE中点G,BD中点F,分别过G,F 做AC,AB的垂线,两垂线交于点H,连接DH, 因为四点C、B、D、E共圆,所以,H为圆心,半径为DH.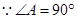 ,
,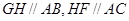 ,所以,
,所以,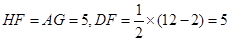 ,
,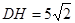
点评:此题考查平面几何中的圆与相似三角形及方程等概念和性质。注意把握判定与性质的作用。

练习册系列答案
相关题目
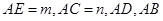 为方程
为方程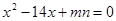 的两根,
的两根,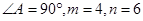 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。
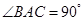 ,
,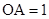 ,
,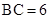 .则⊙O的半径为( ).
.则⊙O的半径为( ).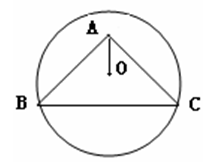
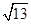 D.
D. 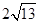
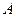 是以
是以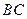 为直径的
为直径的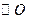 上一点,
上一点,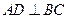 于点
于点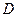 ,过点
,过点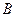 作
作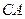 的延长线相交于点
的延长线相交于点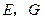 是
是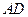 的中点,连结
的中点,连结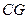 并延长与
并延长与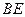 相交于点
相交于点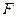 ,延长
,延长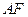 与
与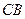 的延长线相交于点
的延长线相交于点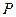 .
.
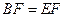 ;
; 是
是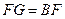 ,且
,且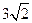 ,求
,求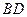 和
和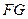 的长度.
的长度.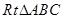 中,
中,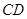 、
、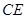 分别是斜边
分别是斜边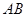 上的高和中线,是该图中共有
上的高和中线,是该图中共有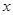 个三角形与
个三角形与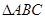 相似,则
相似,则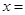 ( )
( )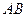 是⊙
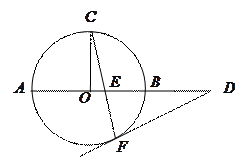
是⊙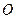 的直径,
的直径,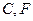 是⊙
是⊙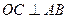 ,过点
,过点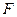 作⊙
作⊙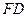 交
交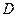 ,连接
,连接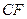 交
交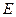 .
. 
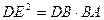
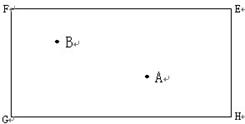
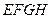 是一个长方形
是一个长方形 台球桌面,有白、黑两球分别位于
台球桌面,有白、黑两球分别位于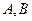 两点的位置上.试问,怎样撞击白球
两点的位置上.试问,怎样撞击白球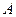 ,才能使
,才能使 白球
白球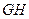 ,再碰撞
,再碰撞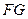 ,经两次反弹后再击中黑球
,经两次反弹后再击中黑球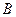 ?
?
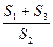 的取值范围是 .
的取值范围是 .